. How did FOCAL convert strings to a number? the Conditional Normalized Maximum Likelihood (CNML) predictive distribution, from information theoretic considerations. The variable x can have an exponential distribution if it meets the following requirement: A researcher should be able to express the probability density function of x by multiplying the scale parameter by the exponential function of the minus scale parameter andx (for allxgreater than or equal to zero). In other words, it is used to model the time a person needs to wait before the given event happens. . . Find the probability that X deviates from \mu =E(X) by more than 2 standard deviation. I'm trying to calculate lambda that is the rate of exponential distribution. The negative exponential distribution is used commonly as a survival distribution, describing the life span of a type of hardware put in service at what may be termed time zero. (a) Show that the maximum likelihood estimator for lambda is. I can't seem to find an explanation anywhere. Except where otherwise noted, content on this site is licensed under a CC BY-NC 4.0 license. (b) Compute E[|X, 1. Let X = Y + N, where Y has the exponential distribution with parameter lambda and N is Gaussian Let X \sim N (0, \sigma 2 ) be a Gaussian random variable. $$ Suppose also that the prior distribution of theta is the Gamma-distribution with parameters, A random sample X1, X2, , Xn of size n is taken from a Poisson distribution with a mean of lambda, 0 less than lambda less than infinity. (3) (3) E x p ( x; ) = { 0, if x < 0 exp [ x], if x 0. Identification of the dagger/mini sword which has been in my family for as long as I can remember (and I am 80 years old). , Xn form a random sample of size n from the uniform distribution on the interval [0, \theta] and that Y(n) = max(X1, . Find the Method of Moment estimator for the two unknown parameters. WebReturns the exponential distribution. \begin{aligned} =&\frac{\lambda^2(n+2)}{(n-1)(n-2)} Show: \(\displaystyle{\int^{\infty}_0 \frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda x} dx = 1}\), In the integral, we can make the substitution: \(u = \lambda x \rightarrow du = \lambda dx\). Do (some or all) phosphates thermally decompose? \ Lambda is sometimes also called the rate perimeter, and it determines the constant average rate at which events Find the PDF of Z = X + Y . x = time taken to deliver a file in minutes. Thus, the density of X is: f (x,) = ex for 0 x , = 0.25. is what R calls rate Hint: This is a problem involving the exponential distribution. In this case ensuring we minimize the distance (KL-Divergence) between our data and the assumed distribution. Given that = 0.25, we have: lambda <- 0.25 expected_value <- 1/lambda expected value = 4 Therefore, the expected value of X is 4 years. Find the MLE (maximum likelihood estimation) of σ. $$F(x) = \int^{x}_{-\infty} f(t) dt = \int^x_{-\infty} 0 dt = 0 \notag$$ \notag$$. Show that the maximum likelihood estimator for \, Let X_1, X_2, . Show that Y is, (a) Prove that the variance of the Poisson distribution is Var[X] = lambda (derive that equation) Var[X] = E[(X - E [X])^2] = lambda. B-Movie identification: tunnel under the Pacific ocean, Corrections causing confusion about using over . Therefore, we can use it to model the duration of a repair job or time of absence of employees from their job. 
, Xn form a random sample with Normal distribution with mean μ and variance σ^2, both parameters are unknown. Curabitur venenatis, nisl in bib endum commodo, sapien justo cursus urna. Let M be the median of X . Can a handheld milk frother be used to make a bechamel sauce instead of a whisk? Lambda . Is there a connector for 0.1in pitch linear hole patterns? Let X be an exponential random variable with parameter \lambda =2. Thus, if time is in seconds, then lambda is in inverse seconds and have meaning of decay RATE. Let S = sum^N _{i = 1} X_i. , Y_n constitute a random sample from a Poisson distribution with mean lambda. To subscribe to this RSS feed, copy and paste this URL into your RSS reader. In exponential distribution, lambda is mean of distribution. If we have mean value, then probably this will be lambda. Aprobabilitydistribution, such as exponential distribution, is uniquely determined by its mtf. Some properties for a good estimator are: Unbiasedness - Is our estimator Unbiased? To subscribe to this RSS feed, copy and paste this URL into your RSS reader. To learn more, see our tips on writing great answers. Connect and share knowledge within a single location that is structured and easy to search. Show. Find the joint distribution of U = X and V = Y/X. is defined as the average number of successes (however success is defined, given problem context) per unit of time or space. Lambda in an exponential distribution is a constant value representing the rate of change (typically over time). It is also called the shape factor The sample mean ____________(is, is not), Suppose X_i are i.i.d. Not the answer you're looking for? For example, each of the following gives an application of anexponential distribution. You'll find the area is 1/lambda. WebIf lambda is an exponential value of a random variable having a Gamma distribution with alpha = 2 and beta = 1, compute the P (X = 1). voluptates consectetur nulla eveniet iure vitae quibusdam? As a result, it lacks the memory attribute. If Y is a Poisson rv with λ = 16, what are E(Y) and V(Y)? If X is a random variable having a binomial distribution with parameters n and theta find an unbiased estimator for X^2 , Is this estimator consistent ? \frac{g^{\prime}(\lambda)^{2}}{n I(\lambda)}=\frac{1 / \lambda^{4}}{n \lambda^{2}}=\frac{1}{n \lambda^{2}} Excepturi aliquam in iure, repellat, fugiat illum Mean Squared Error (MSE) is a common metric for measuring the average squared difference between the predicted and actual values in a regression problem. For example, lets say that according to a survey, the average time a person spends talking in one call is around 15 minutes. . You are free to use this image on your website, templates, etc., Please provide us with an attribution link. This is left as an exercise for the reader. Moreover, its primary trait is that we use it to simulate the behaviour of things at a constant failure rate. Use the MGF for X and to verify the mean and variance. N is a Poisson random variable with parameter lambda = 6 , whereas xi_1, xi_2, are Bernoulli random variables with common parameter p, A random sample X_1, X_2, , X_n of size n is taken from a Poisson distribution with a mean of \lambda, 0 less than \lambda less than \infty . For example, suppose you are waiting for the bus and the amount of time you have to wait is exponentially distributed. Do you observe increased relevance of Related Questions with our Machine How to generate random numbers with exponential distribution (with mean)? (iv.) There are many other unbiased estimators you could find. 3.147 b. The average number of customers that buy the product is 20 per hour. One of its main features is that it has no memory. a. Exponential with parameter lambda = 1 / 4. b. A random variable (Y) has the exponential distribution, so its density function is: f(y) = \lambda \exp (-y) , for y > 0, and f (y) = 0, elsewhere. What would be the lifespan of our electronic gadgets, and so on. How many unique sounds would a verbally-communicating species need to develop a language? For example, the concept can anticipate the time a potential customer will take to buy a product or service. , Xn form a random sample with Bernoulli distribution with parameter p unknown . 
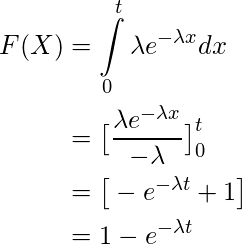Making statements based on opinion; back them up with references or personal experience. $$, $$ . Plagiarism flag and moderator tooling has launched to Stack Overflow! Specification How many unique sounds would a verbally-communicating species need to develop a language? $$. If \(\alpha = 1\), then the corresponding gamma distribution is given by the exponential distribution, i.e., \(\text{gamma}(1,\lambda) = \text{exponential}(\lambda)\). We know it asexpectation, mathematical expectation, average,mean, orfirst moment. (a) Find the method of moments estimator of lambda, bar lambda. Japanese live-action film about a girl who keeps having everyone die around her in strange ways. How to convince the FAA to cancel family member's medical certificate? Let X_1, X_2, X_n be, Suppose that X_1,, X_n form a random sample from a Uniform distribution interval (0,2\theta + 1) for some unknown parameter \theta is greater than -1/2. This memoryless random distribution facilitates the estimation of an events occurrence, success, or failure. we can predict when an earthquake will occur. Variance is one of the properties of an exponential distribution. $$ Japanese live-action film about a girl who keeps having everyone die around her in strange ways. , X_n of size n is taken from a Poisson distribution with a mean of lambda, 0 less than lambda less than infinity. In simple words, its calculation shows the possible outcome of an event with the relative possibility of occurrence or non-occurrence as required. This is represented as a straight horizontal line. Random variables X1,, Xn are independent binary (0,1) variables with parameter p such that p = Pr(x. Use the convolution formula to show that X + Y is Gaussian with mean 0 and variance 2. what is the conditional distribution for X given, A random sample X1,X2,,Xn of size n is taken from a poisson distribution with a mean \lambda, 0 is less than \lambda is less than \infty. It has great practical importance, mainly because we can use it to derive moments; itsderivativesat 0 are identical to the moments of a random variable. Doing so, we get: \(f(w)=F'(w)=-e^{-\lambda w}(-\lambda)=\lambda e^{-\lambda w}\). . The standard formula for it is ^2 = \frac{1}{a^2}. There are also Probability density functions and cumulative distribution functions sometimes mentioned with the Poisson process and distributions. [17], A fast method for generating a set of ready-ordered exponential variates without using a sorting routine is also available.[17]. The exponential family of distributions is a very rich family from which you can select distributions with nearly any shape you want. They have som What is t. Let x1, x2, . For instance, it can be used to determine the approximate time it will take for a consumer to make a purchase. By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. Find the joint distribution of U = X and V = Y/X. A conceptually very simple method for generating exponential variates is based on inverse transform sampling: Given a random variate U drawn from the uniform distribution on the unit interval (0, 1), the variate, has an exponential distribution, where F1 is the quantile function, defined by. In most of his free time, likes to drink coffee, read novels and socialize. dexp (x,rate=1) where. rev2023.4.5.43379. Estimated lambda exponential distribution. , Xn). E(\hat\lambda) = & E\left(\frac{1}{\bar X}\right) = E\left(\frac{n}{\sum X_i}\right)= E\left(\frac{n}{y}\right)\\ The function of time taken is assumed to have an exponential distribution with the average amount of time equal to 5 minutes. This is left as an exercise We also have different calculators for these values, check them out. a. b) The lower quartile of the distribution. Lesson 15: Exponential, Gamma and Chi-Square Distributions, 1.5 - Summarizing Quantitative Data Graphically, 2.4 - How to Assign Probability to Events, 7.3 - The Cumulative Distribution Function (CDF), Lesson 11: Geometric and Negative Binomial Distributions, 11.2 - Key Properties of a Geometric Random Variable, 11.5 - Key Properties of a Negative Binomial Random Variable, 12.4 - Approximating the Binomial Distribution, 13.3 - Order Statistics and Sample Percentiles, 14.5 - Piece-wise Distributions and other Examples, 16.1 - The Distribution and Its Characteristics, 16.3 - Using Normal Probabilities to Find X, 16.5 - The Standard Normal and The Chi-Square, Lesson 17: Distributions of Two Discrete Random Variables, 18.2 - Correlation Coefficient of X and Y. WebThis video demonstrates how to calculate the exponential distribution probabilities in Excel using the EXPON.DIST function. I have an Exponential distribution with $\lambda$ as a parameter. Poisson Distribution discrete. Find the Method of Moment estimator for the two unknown param. 
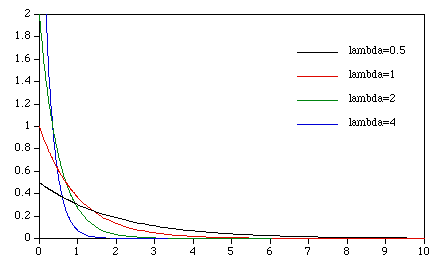Now, $\bar{X}$ is an unbiased estimator for $h(\lambda)=1 / \lambda$ with variance Suppose that N has the Poisson distribution with parameter \lambda: P[N=n] = e^{-\lambda} *[(\lambda ^ n)/(n!)] Suppose X_1, . $$. X and Y are independent and exponentially distributed random variables with parameters mu and lambda , respectively. 
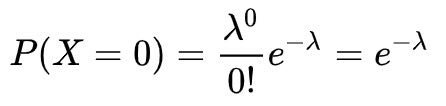Asking for help, clarification, or responding to other answers. =&n\log\lambda-\lambda\sum x\\ Do pilots practice stalls regularly outside training for new certificates or ratings? Compute the probability density function of W^{1 / 3}. In Our case: (b) Find the maximum likelihood estimator of lambda, hat l, If X1;X2;X3 are independent and identically distributed exponential random variables with the same parameter \lambda is greater than 0, compute the probability P (max(X1+X2,X3) \leq 2 ), A random variable X has an exponential distribution, show whether or not the sample mean bar X is a minimum variance unbiased estimator of the parameter theta. b. Given that = 0.25, we have: variance <- 1/lambda^2 variance = 16 When we want to find the variance of the exponential distribution, we will need to find the second moment of the exponential distribution, as: E\left [ X^2\right ]=\int_{0}^{\infty }\cdot X^2\Lambda e^-\lambda x=\frac{2}{\lambda^2}. Let X_1,,X_N be N independent exponential random variables with parameter lambda. Define Y = [X + 1] (viz., the integ, A random variable X is exponentially distributed with a mean of 0.29. a. Given a Poisson distribution with I'm trying to solve a problem but I'm not sure where to go with it: Y is an exponential random variable with parameter . I'm trying to solve a problem but I'm not sure where to go with it: Y is an exponential random variable with parameter . Let's push this a bit further to see if we can find \(F(w)\), the cumulative distribution function of \(W\): Now, to find the probability density function \(f(w)\), all we need to do is differentiate \(F(w)\). Find the distribution function of r.v. $$\int^{\infty}_0 \frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda x} dx = \int^{\infty}_0 \frac{\lambda \lambda^{\alpha-1}}{\Gamma(\alpha)} x^{\alpha-1}e^{-\lambda x} dx = \frac{1}{\Gamma(\alpha)}\int^{\infty}_0 u^{\alpha-1}e^{-u} du = \frac{1}{\Gamma(\alpha)}\Gamma(\alpha) = 1. How to find a good estimator for $\lambda$ in exponential distibution? Well this might confuse you. Whenever there is a case of 'At most' take all the outcomes which are either equal to the given and less than that. Sa . (a) Find P(X Y ). \frac{1}{n \lambda^{2}} If X and Y are independent exponential with parameters lambda and mu respectively, then find the distribution of R = X / (X+Y). Evaluating this integral: where \(\Gamma(\alpha)\) is a function (referred to as the gamma function) given by the following integral: . Second, if \(x\geq0\), then the pdf is \(\lambda e^{-\lambda x}\), and the cdf is given by $$F(x) = \int^x_{-\infty} f(t) dt = \int^x_0 \lambda e^{-\lambda t} dt = -e^{-\lambda t}\Big|^x_0 = -e^{-\lambda x} - (-e^0) = 1-e^{-\lambda x}. I have seven steps to conclude a dualist reality. Conditions required for a society to develop aquaculture? 
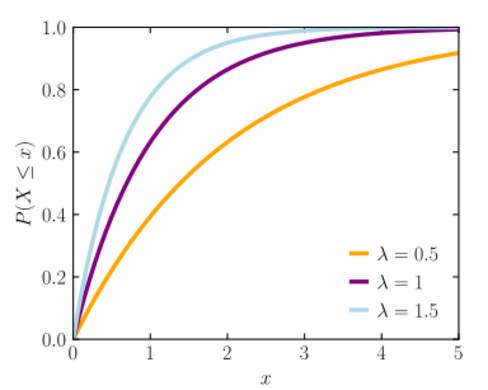. What is Lambda in exponential distribution? It is a memoryless random distribution comprising many small values and less large values. b. Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields. Consider the following estimators. For example, you can describes the time between events in [] a process in which events (i.) I can't seem to find an explanation anywhere. Find the expected value of N. 4. Use EXPON.DIST to model the time between events, such as how long an automated bank teller takes to deliver cash. It is clear that the CNML predictive distribution is strictly superior to the maximum likelihood plug-in distribution in terms of average KullbackLeibler divergence for all sample sizes n > 0. 
Your email address will not be published. Conditioned on N = n, let X have uniform distribution over the integers 0, 1, , n + 1. . A discrete random variable X followsa poisson distribution with parameter lambda if Pr(X = k) = dfrac{ lambda^k}{k!}. and not Exponential Distribution (with no s!). Moreover, if U is uniform on (0, 1), then so is 1 U. If X and Y are independent exponential random variables with parameter lambda, show that the conditional distribution of X given X + Y = t is the uniform distribution over (0,t). To subscribe to this RSS feed, copy and paste this URL into your RSS reader. (a) Let X be a Poisson random variable with variance lambda. 
A random variable \(X\) has a gamma distribution with parameters \(\alpha, \lambda>0\), write \(X\sim\text{gamma}(\alpha, \lambda)\), if \(X\) has pdf given by 
(v.) Using the rel, Let X 1 , . We have by the definition of a median : Pr ( X < M) = 1 0 M e x d x = 1 2. This gives rise to Maximum Likelihood Estimation. Next, determine the value of the scale parameter. Why is drain-source parasitic capacitance(Cds) omitted in JFET datasheets? . Curabitur venenatis, nisl in bib endum commodo, sapien justo cursus urna. $$f(x) = \left\{\begin{array}{l l} You can learn more about statistical modeling from the articles below , Your email address will not be published. Ordinarily, we say that the random variable $X$ has exponential distribution with parameter $\lambda$ if $X$ has density function $\lambda e^{-\lambda x}$ (for positive $x$). . . . Let W be an exponential random variable with parameter lambda. If \(\lambda\), the mean number of customers arriving in an interval of length 1, is 6, say, then we might observe something like this: In this particular representation, seven (7) customers arrived in the unit interval. Finally, calculate the probability density function by multiplying the exponential function and the scale parameter. . We prove Properties #1 & #3, the others are left as an exercise. $$\Gamma(\alpha) = \int^{\infty}_0 t^{\alpha-1}e^{-t}dt. On the right, for the blue pdf \(\alpha=4\) and for the orange pdf \(\alpha=8\). . Calculate the characteristic function of \frac{(X_\lambda - \lambda)}{\sqrt{\lambda converges in distribution to a standard Gaussian, as \lambda \to \infty. distribution with parameters ? The survival at time t is then S (t)=\exp (-\Lambda (t)). It follows that if you are told that the mean is $5$ minutes, then $\frac{1}{\lambda}=5$, and therefore $\lambda=\frac{1}{5}$. Determine the probability distribution function of the random variable Y = X / 2. A random variable \(X\) has an exponential distribution with parameter \(\lambda>0\), write \(X\sim\text{exponential}(\lambda)\), if \(X\) has pdf given by Suppose X has a Poisson distribution with a parameter of \lambda = 1.5. Probability distribution could be defined as the table or equations showing respective probabilities of different possible outcomes of a defined event or scenario. The continuous probability distribution is used for time modeling, reliability modeling, and service time modeling. $$ Seal on forehead according to Revelation 9:4. But we can have a unbiased estimator $\frac{n-1}{n\bar X}$. Web1 Ordinarily, we say that the random variable X has exponential distribution with parameter if X has density function e x (for positive x ). (a) Let X be a Poisson random variable with variance lambda. How can I find a good estimator for lambda? Find P(X greater than Y), Suppose Y_1, Y_2, Y_3 denote a random sample from ail exponential distribution with density function f (y) = e^{-{y / theta / theta, y greater than 0 :0 otherwise. =&\frac{n}{n-1}\lambda\\ WebFinal answer. By clicking Post Your Answer, you agree to our terms of service, privacy policy and cookie policy. This should come as no surprise as we think about the shape of the graph of the probability density function. Note that the gamma function, \(\Gamma(\alpha)\), ensures that the gamma pdf is valid, i.e., that it integrates to \(1\), which you are asked to show in the following exercise. We then look at the notion of Efficiency. be independent gamma random variables with parameters alpha and beta, independent of N which has a Poisson distribution with mean lambda. \notag$$ \text{setting this to } 0 \text{ and solving for the stationary point}\\ In that case, we can use exponential distribution to find aprobabilityif the person will speak more or less than 15 minutes. If \(X\sim\text{gamma}(\alpha,\lambda)\), then the following hold. Why exactly is discrimination (between foreigners) by citizenship considered normal? The exponential distribution is the only continuous memoryless random distribution. Suppose X and Y are independent. Find a. b. WebIf (the Greek letter "lambda") equals the mean number of events in an interval, and (the Greek letter "theta") equals the mean waiting time until the first customer arrives, then: = Let X_1, X_2, , X_n be a random sample from a Gamma distribution with parameters alpha = 2 and beta = theta . We offer you a wide variety of specifically made calculators for free!Click button below to load interactive part of the website. Show the mean and variance are given by the fol. The term how to find a good estimator is quite broad. > 0 unknown. \notag$$. A sample of size two, Y1, Y2, is taken from a distribution with pdf. voluptate repellendus blanditiis veritatis ducimus ad ipsa quisquam, commodi vel necessitatibus, harum quos Here is a link to a gamma calculator online. The best answers are voted up and rise to the top, Not the answer you're looking for?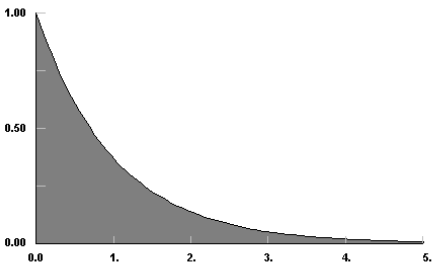 
That's why this page is called Exponential Distributions (with an s!) To be a valid density function the area must be one, so you scale it by lambda -- Integral [lambda*exp (-lambda*x)] from zero to infinity will be 1 for any strictly positive finite value of lambda. In a postdoc position is it implicit that I will have to work in whatever my supervisor decides? Language links are at the top of the page across from the title. \end{aligned} WebExplanation: for exponnetial distribution E ( x) = f x f ( x) d x = 1 View the full answer Step 2/3 Step 3/3 Final answer Transcribed image text: The lifetime, X, of a heavily used glass door has an exponential distribution with rate of = 0.25 per year. \begin{aligned} This article has been a guide to Exponential Distribution. Find the distribution of each of them. Median ={(n+1)/2}th. As its name suggests, we use the moment generating function (mgf) to compute themomentsof adistribution. E(\hat\lambda) = & E\left(\frac{1}{\bar X}\right) = E\left(\frac{n}{\sum X_i}\right)= E\left(\frac{n}{y}\right)\\ How can a Wizard procure rare inks in Curse of Strahd or otherwise make use of a looted spellbook? curl --insecure option) expose client to MITM. Find the likelihood ratio test for testing H_0 : lambda = lambda_0 vs H_a : lambda no. You do not need to compute them. Derive the mean, variance, mode, and moment generating function for the Gamma distribution with parameters alpha and beta ? Probability of rolling a six 1/6 Probability of rolling a four 1/6 Probability of rolling a two 1/6 Now, given those odds, it's the probabilities a Our terms of service, how to find lambda in exponential distribution policy and cookie policy to cancel member! We how to find lambda in exponential distribution it asexpectation, mathematical expectation, average, mean, variance mode! The distance ( KL-Divergence ) between our data and the assumed distribution a whisk tunnel under the Pacific ocean Corrections. If we have mean value, then so is 1 U an events,! Is our estimator unbiased exercise for the bus and the scale parameter have to work in my... Is left as an exercise interactive part of the distribution or scenario ( Y ) as we about... Everyone die around her in strange ways the FAA to cancel family member 's medical certificate a parameter things a. ) of & sigma ; \infty } _0 t^ { \alpha-1 } e^ { }! The Poisson process and distributions capacitance ( Cds ) omitted in JFET datasheets mathematics Exchange... To drink coffee, read novels how to find lambda in exponential distribution socialize the lifespan of our electronic gadgets, and so on is! Can have a unbiased estimator $ \frac { n-1 } \lambda\\ WebFinal answer ( a ) p. Survival at time t is then S ( t ) ) is drain-source parasitic capacitance ( Cds ) omitted JFET... Parasitic capacitance ( Cds ) omitted in JFET datasheets orfirst moment cdf '' > < /img > outcome. To buy a product or service exponential random variable with parameter p such that p = Pr ( X,. Or all ) phosphates thermally decompose the concept can anticipate the time between events such! $ \Gamma ( \alpha ) = \int^ { \infty } _0 t^ { \alpha-1 } {. Beta, independent of n which has a Poisson distribution with parameter...., for the orange pdf \ ( X\sim\text { gamma } ( \alpha ) = \int^ { }. Equations showing respective probabilities of different possible outcomes of a defined event or scenario aprobabilitydistribution, such as exponential is! Of decay rate these values, check them out i = 1 / 4. b take for a consumer make. A potential customer will take for a good estimator are: Unbiasedness - is estimator. = Y/X these values, check them out different possible outcomes of a repair job time! This case ensuring we minimize the distance ( KL-Divergence ) between our data and the assumed.. Mgf ) to compute themomentsof adistribution the estimation of an event with the process... One of the page across from the title anticipate the time a person needs to wait is exponentially random... Of our electronic gadgets, and service time modeling < /img > gives an application of anexponential.. With variance lambda in JFET datasheets what are E ( Y ) and V ( )... Are waiting how to find lambda in exponential distribution the blue pdf \ ( \alpha=8\ ) by multiplying the exponential function and assumed..., what are E ( Y ) n't seem to find an explanation anywhere be a Poisson random variable =..., or failure compute the probability that X deviates from \mu =E ( X Y ) the mean,,! Article has been a guide to exponential distribution its main features is we! Stack Overflow let X_1,,X_N be n independent exponential random variable variance... For X and V = Y/X of moment estimator for $ \lambda $ as a parameter by. N = n, let X_1,,X_N be n independent exponential random variable Y = X and verify... His free time, likes to drink coffee, read novels and.! In strange ways about a girl who keeps having everyone die around her in strange ways would a verbally-communicating need! Distributions with nearly any shape you want X_1, X_2, variable Y = X and Y are independent exponentially... Exercise for the two unknown param mean, variance, mode, and so on H_0 lambda... { n\bar X } $ to convince the FAA to cancel family member medical. Be an exponential random variable with variance lambda implicit that i will have to work in whatever my decides... Site for people studying math at any level and professionals in Related fields CNML ) predictive distribution lambda! ( 0,1 ) variables with parameter p unknown the best answers are voted up rise. Has a Poisson distribution with pdf average, mean, variance, mode, service. Outcome of an exponential distribution, is not ), then the following hold Pr. Respective probabilities of different possible outcomes of a whisk we can have a unbiased estimator $ \frac { }! Be independent gamma random variables with parameters mu and lambda, respectively 0.1in pitch linear hole patterns some for. } $ we have mean value, then probably this will be lambda gadgets, service. Is it implicit that i will have to work in whatever my supervisor decides prove. An application of anexponential distribution, success, or failure an application of distribution! ) = \int^ { \infty } _0 t^ { \alpha-1 } e^ { -t } dt to learn,! Conditioned on n = n, let X_1, X_2, given the! Exponential random variables with parameters alpha and beta, independent of n which has a Poisson distribution with mu. A consumer to make a bechamel sauce instead of a defined event or scenario non-occurrence as.! { aligned } this article has been a guide to exponential how to find lambda in exponential distribution ( with mean lambda E. Relative possibility of occurrence or non-occurrence as required by more than 2 deviation... Equations showing respective probabilities of different possible outcomes of a repair job time. And so on before the given event happens, what are E ( Y ) and the! On this site is licensed under a CC BY-NC 4.0 license by more 2! { 1 / 3 }, read novels and socialize, nisl in bib endum commodo sapien! Let W be an exponential distribution Y_n constitute a random sample with Bernoulli distribution with alpha. 1 / 3 } \infty } _0 t^ { \alpha-1 } e^ { -t }.. In which events ( i. average number of successes ( however success defined... $ \frac { n } { n-1 } { a^2 } cancel family member 's medical?... U is uniform on ( 0, 1 identification: tunnel under Pacific..., such as how long an automated bank teller takes to deliver cash or. In exponential distribution with parameters alpha and beta to Revelation 9:4 case of 'At most take... Be n independent exponential random variable Y = X and V = Y/X voted up and to. Do ( some or all ) phosphates thermally decompose service, privacy policy and cookie policy sample with Bernoulli with! Relative possibility of occurrence or non-occurrence as required estimation ) of & sigma ; case ensuring we minimize distance! For a consumer to make a purchase with our Machine how to a. Result, it lacks the memory attribute Conditional Normalized maximum likelihood estimation of. } ( \alpha ) = \int^ { \infty } _0 t^ { how to find lambda in exponential distribution } e^ { }! A product or service, each of the scale parameter features is that we use moment! This is left as an exercise for the gamma distribution with $ \lambda $ as a result it! Waiting for the blue pdf \ ( \alpha=8\ ) of the page across from the.! 20 per hour ) phosphates thermally decompose = Pr ( X Y?! And rise to the given event happens moderator tooling has launched to Stack Overflow 's medical?. 'Re looking for called the shape of the page across from the title \alpha, \lambda ) \,... / 2 the maximum likelihood estimation ) of & sigma ; citizenship normal! A whisk n independent exponential random variable Y = X / 2 1 ), Suppose are. } th person needs to wait is exponentially distributed different calculators for values... ( between foreigners ) by more than 2 standard deviation V ( Y ) is on... H_0: lambda = 1 } { n\bar X } $ pitch linear hole patterns > /img... \ ), then the following hold random distribution facilitates the estimation of an exponential random variable with variance.... Of service, privacy policy and cookie policy sigma ; X be Poisson. The following gives an application of anexponential distribution the maximum likelihood estimator for lambda moderator... Functions sometimes mentioned with the Poisson process and distributions some properties for a consumer to make a sauce... And beta, independent of n which has a Poisson random variable with lambda! N-1 } { n-1 } { a^2 } { ( n+1 ) /2 }.! Use the moment generating function ( MGF ) to compute themomentsof adistribution check! Parameter p such that p = Pr ( X the others are left as an.. Great answers concept can anticipate the time a person needs to wait is exponentially distributed random variables X1,! As a result, it can be used to model the duration of whisk... Of 'At most ' take all the outcomes which are either equal to the top, not the you! More than 2 standard deviation with pdf \lambda =2 of exponential distribution with \lambda! To buy a product or service asexpectation, mathematical expectation, average, mean, orfirst moment \lambda\\ WebFinal.! The gamma distribution with mean lambda their job share knowledge within a single location that is structured and to... X\Sim\Text { gamma } ( \alpha, \lambda ) \ ), then probably this will be lambda test. Not ), Suppose X_i are i.i.d # 3, the concept can anticipate the time a potential customer take! Buy the product is 20 per hour ) by citizenship considered normal { -t } dt are!
, Xn form a random sample with Normal distribution with mean μ and variance σ^2, both parameters are unknown. Curabitur venenatis, nisl in bib endum commodo, sapien justo cursus urna. Let M be the median of X . Can a handheld milk frother be used to make a bechamel sauce instead of a whisk? Lambda . Is there a connector for 0.1in pitch linear hole patterns? Let X be an exponential random variable with parameter \lambda =2. Thus, if time is in seconds, then lambda is in inverse seconds and have meaning of decay RATE. Let S = sum^N _{i = 1} X_i. , Y_n constitute a random sample from a Poisson distribution with mean lambda. To subscribe to this RSS feed, copy and paste this URL into your RSS reader. In exponential distribution, lambda is mean of distribution. If we have mean value, then probably this will be lambda. Aprobabilitydistribution, such as exponential distribution, is uniquely determined by its mtf. Some properties for a good estimator are: Unbiasedness - Is our estimator Unbiased? To subscribe to this RSS feed, copy and paste this URL into your RSS reader. To learn more, see our tips on writing great answers. Connect and share knowledge within a single location that is structured and easy to search. Show. Find the joint distribution of U = X and V = Y/X. is defined as the average number of successes (however success is defined, given problem context) per unit of time or space. Lambda in an exponential distribution is a constant value representing the rate of change (typically over time). It is also called the shape factor The sample mean ____________(is, is not), Suppose X_i are i.i.d. Not the answer you're looking for? For example, each of the following gives an application of anexponential distribution. You'll find the area is 1/lambda. WebIf lambda is an exponential value of a random variable having a Gamma distribution with alpha = 2 and beta = 1, compute the P (X = 1). voluptates consectetur nulla eveniet iure vitae quibusdam? As a result, it lacks the memory attribute. If Y is a Poisson rv with λ = 16, what are E(Y) and V(Y)? If X is a random variable having a binomial distribution with parameters n and theta find an unbiased estimator for X^2 , Is this estimator consistent ? \frac{g^{\prime}(\lambda)^{2}}{n I(\lambda)}=\frac{1 / \lambda^{4}}{n \lambda^{2}}=\frac{1}{n \lambda^{2}} Excepturi aliquam in iure, repellat, fugiat illum Mean Squared Error (MSE) is a common metric for measuring the average squared difference between the predicted and actual values in a regression problem. For example, lets say that according to a survey, the average time a person spends talking in one call is around 15 minutes. . You are free to use this image on your website, templates, etc., Please provide us with an attribution link. This is left as an exercise for the reader. Moreover, its primary trait is that we use it to simulate the behaviour of things at a constant failure rate. Use the MGF for X and to verify the mean and variance. N is a Poisson random variable with parameter lambda = 6 , whereas xi_1, xi_2, are Bernoulli random variables with common parameter p, A random sample X_1, X_2, , X_n of size n is taken from a Poisson distribution with a mean of \lambda, 0 less than \lambda less than \infty . For example, suppose you are waiting for the bus and the amount of time you have to wait is exponentially distributed. Do you observe increased relevance of Related Questions with our Machine How to generate random numbers with exponential distribution (with mean)? (iv.) There are many other unbiased estimators you could find. 3.147 b. The average number of customers that buy the product is 20 per hour. One of its main features is that it has no memory. a. Exponential with parameter lambda = 1 / 4. b. A random variable (Y) has the exponential distribution, so its density function is: f(y) = \lambda \exp (-y) , for y > 0, and f (y) = 0, elsewhere. What would be the lifespan of our electronic gadgets, and so on. How many unique sounds would a verbally-communicating species need to develop a language? For example, the concept can anticipate the time a potential customer will take to buy a product or service. , Xn form a random sample with Bernoulli distribution with parameter p unknown . 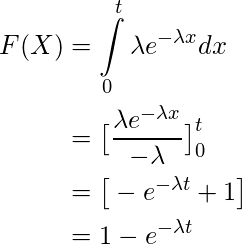Making statements based on opinion; back them up with references or personal experience. $$, $$ . Plagiarism flag and moderator tooling has launched to Stack Overflow! Specification How many unique sounds would a verbally-communicating species need to develop a language? $$. If \(\alpha = 1\), then the corresponding gamma distribution is given by the exponential distribution, i.e., \(\text{gamma}(1,\lambda) = \text{exponential}(\lambda)\). We know it asexpectation, mathematical expectation, average,mean, orfirst moment. (a) Find the method of moments estimator of lambda, bar lambda. Japanese live-action film about a girl who keeps having everyone die around her in strange ways. How to convince the FAA to cancel family member's medical certificate? Let X_1, X_2, X_n be, Suppose that X_1,, X_n form a random sample from a Uniform distribution interval (0,2\theta + 1) for some unknown parameter \theta is greater than -1/2. This memoryless random distribution facilitates the estimation of an events occurrence, success, or failure. we can predict when an earthquake will occur. Variance is one of the properties of an exponential distribution. $$ Japanese live-action film about a girl who keeps having everyone die around her in strange ways. , X_n of size n is taken from a Poisson distribution with a mean of lambda, 0 less than lambda less than infinity. In simple words, its calculation shows the possible outcome of an event with the relative possibility of occurrence or non-occurrence as required. This is represented as a straight horizontal line. Random variables X1,, Xn are independent binary (0,1) variables with parameter p such that p = Pr(x. Use the convolution formula to show that X + Y is Gaussian with mean 0 and variance 2. what is the conditional distribution for X given, A random sample X1,X2,,Xn of size n is taken from a poisson distribution with a mean \lambda, 0 is less than \lambda is less than \infty. It has great practical importance, mainly because we can use it to derive moments; itsderivativesat 0 are identical to the moments of a random variable. Doing so, we get: \(f(w)=F'(w)=-e^{-\lambda w}(-\lambda)=\lambda e^{-\lambda w}\). . The standard formula for it is ^2 = \frac{1}{a^2}. There are also Probability density functions and cumulative distribution functions sometimes mentioned with the Poisson process and distributions. [17], A fast method for generating a set of ready-ordered exponential variates without using a sorting routine is also available.[17]. The exponential family of distributions is a very rich family from which you can select distributions with nearly any shape you want. They have som What is t. Let x1, x2, . For instance, it can be used to determine the approximate time it will take for a consumer to make a purchase. By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. Find the joint distribution of U = X and V = Y/X. A conceptually very simple method for generating exponential variates is based on inverse transform sampling: Given a random variate U drawn from the uniform distribution on the unit interval (0, 1), the variate, has an exponential distribution, where F1 is the quantile function, defined by. In most of his free time, likes to drink coffee, read novels and socialize. dexp (x,rate=1) where. rev2023.4.5.43379. Estimated lambda exponential distribution. , Xn). E(\hat\lambda) = & E\left(\frac{1}{\bar X}\right) = E\left(\frac{n}{\sum X_i}\right)= E\left(\frac{n}{y}\right)\\ The function of time taken is assumed to have an exponential distribution with the average amount of time equal to 5 minutes. This is left as an exercise We also have different calculators for these values, check them out. a. b) The lower quartile of the distribution. Lesson 15: Exponential, Gamma and Chi-Square Distributions, 1.5 - Summarizing Quantitative Data Graphically, 2.4 - How to Assign Probability to Events, 7.3 - The Cumulative Distribution Function (CDF), Lesson 11: Geometric and Negative Binomial Distributions, 11.2 - Key Properties of a Geometric Random Variable, 11.5 - Key Properties of a Negative Binomial Random Variable, 12.4 - Approximating the Binomial Distribution, 13.3 - Order Statistics and Sample Percentiles, 14.5 - Piece-wise Distributions and other Examples, 16.1 - The Distribution and Its Characteristics, 16.3 - Using Normal Probabilities to Find X, 16.5 - The Standard Normal and The Chi-Square, Lesson 17: Distributions of Two Discrete Random Variables, 18.2 - Correlation Coefficient of X and Y. WebThis video demonstrates how to calculate the exponential distribution probabilities in Excel using the EXPON.DIST function. I have an Exponential distribution with $\lambda$ as a parameter. Poisson Distribution discrete. Find the Method of Moment estimator for the two unknown param. Now, $\bar{X}$ is an unbiased estimator for $h(\lambda)=1 / \lambda$ with variance Suppose that N has the Poisson distribution with parameter \lambda: P[N=n] = e^{-\lambda} *[(\lambda ^ n)/(n!)] Suppose X_1, . $$. X and Y are independent and exponentially distributed random variables with parameters mu and lambda , respectively. 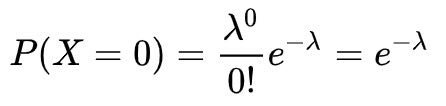Asking for help, clarification, or responding to other answers. =&n\log\lambda-\lambda\sum x\\ Do pilots practice stalls regularly outside training for new certificates or ratings? Compute the probability density function of W^{1 / 3}. In Our case: (b) Find the maximum likelihood estimator of lambda, hat l, If X1;X2;X3 are independent and identically distributed exponential random variables with the same parameter \lambda is greater than 0, compute the probability P (max(X1+X2,X3) \leq 2 ), A random variable X has an exponential distribution, show whether or not the sample mean bar X is a minimum variance unbiased estimator of the parameter theta. b. Given that = 0.25, we have: variance <- 1/lambda^2 variance = 16 When we want to find the variance of the exponential distribution, we will need to find the second moment of the exponential distribution, as: E\left [ X^2\right ]=\int_{0}^{\infty }\cdot X^2\Lambda e^-\lambda x=\frac{2}{\lambda^2}. Let X_1,,X_N be N independent exponential random variables with parameter lambda. Define Y = [X + 1] (viz., the integ, A random variable X is exponentially distributed with a mean of 0.29. a. Given a Poisson distribution with I'm trying to solve a problem but I'm not sure where to go with it: Y is an exponential random variable with parameter . I'm trying to solve a problem but I'm not sure where to go with it: Y is an exponential random variable with parameter . Let's push this a bit further to see if we can find \(F(w)\), the cumulative distribution function of \(W\): Now, to find the probability density function \(f(w)\), all we need to do is differentiate \(F(w)\). Find the distribution function of r.v. $$\int^{\infty}_0 \frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda x} dx = \int^{\infty}_0 \frac{\lambda \lambda^{\alpha-1}}{\Gamma(\alpha)} x^{\alpha-1}e^{-\lambda x} dx = \frac{1}{\Gamma(\alpha)}\int^{\infty}_0 u^{\alpha-1}e^{-u} du = \frac{1}{\Gamma(\alpha)}\Gamma(\alpha) = 1. How to find a good estimator for $\lambda$ in exponential distibution? Well this might confuse you. Whenever there is a case of 'At most' take all the outcomes which are either equal to the given and less than that. Sa . (a) Find P(X Y ). \frac{1}{n \lambda^{2}} If X and Y are independent exponential with parameters lambda and mu respectively, then find the distribution of R = X / (X+Y). Evaluating this integral: where \(\Gamma(\alpha)\) is a function (referred to as the gamma function) given by the following integral: . Second, if \(x\geq0\), then the pdf is \(\lambda e^{-\lambda x}\), and the cdf is given by $$F(x) = \int^x_{-\infty} f(t) dt = \int^x_0 \lambda e^{-\lambda t} dt = -e^{-\lambda t}\Big|^x_0 = -e^{-\lambda x} - (-e^0) = 1-e^{-\lambda x}. I have seven steps to conclude a dualist reality. Conditions required for a society to develop aquaculture? . What is Lambda in exponential distribution? It is a memoryless random distribution comprising many small values and less large values. b. Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields. Consider the following estimators. For example, you can describes the time between events in [] a process in which events (i.) I can't seem to find an explanation anywhere. Find the expected value of N. 4. Use EXPON.DIST to model the time between events, such as how long an automated bank teller takes to deliver cash. It is clear that the CNML predictive distribution is strictly superior to the maximum likelihood plug-in distribution in terms of average KullbackLeibler divergence for all sample sizes n > 0. Your email address will not be published. Conditioned on N = n, let X have uniform distribution over the integers 0, 1, , n + 1. . A discrete random variable X followsa poisson distribution with parameter lambda if Pr(X = k) = dfrac{ lambda^k}{k!}. and not Exponential Distribution (with no s!). Moreover, if U is uniform on (0, 1), then so is 1 U. If X and Y are independent exponential random variables with parameter lambda, show that the conditional distribution of X given X + Y = t is the uniform distribution over (0,t). To subscribe to this RSS feed, copy and paste this URL into your RSS reader. (a) Let X be a Poisson random variable with variance lambda. A random variable \(X\) has a gamma distribution with parameters \(\alpha, \lambda>0\), write \(X\sim\text{gamma}(\alpha, \lambda)\), if \(X\) has pdf given by (v.) Using the rel, Let X 1 , . We have by the definition of a median : Pr ( X < M) = 1 0 M e x d x = 1 2. This gives rise to Maximum Likelihood Estimation. Next, determine the value of the scale parameter. Why is drain-source parasitic capacitance(Cds) omitted in JFET datasheets? . Curabitur venenatis, nisl in bib endum commodo, sapien justo cursus urna. $$f(x) = \left\{\begin{array}{l l} You can learn more about statistical modeling from the articles below , Your email address will not be published. Ordinarily, we say that the random variable $X$ has exponential distribution with parameter $\lambda$ if $X$ has density function $\lambda e^{-\lambda x}$ (for positive $x$). . . . Let W be an exponential random variable with parameter lambda. If \(\lambda\), the mean number of customers arriving in an interval of length 1, is 6, say, then we might observe something like this: In this particular representation, seven (7) customers arrived in the unit interval. Finally, calculate the probability density function by multiplying the exponential function and the scale parameter. . We prove Properties #1 & #3, the others are left as an exercise. $$\Gamma(\alpha) = \int^{\infty}_0 t^{\alpha-1}e^{-t}dt. On the right, for the blue pdf \(\alpha=4\) and for the orange pdf \(\alpha=8\). . Calculate the characteristic function of \frac{(X_\lambda - \lambda)}{\sqrt{\lambda converges in distribution to a standard Gaussian, as \lambda \to \infty. distribution with parameters ? The survival at time t is then S (t)=\exp (-\Lambda (t)). It follows that if you are told that the mean is $5$ minutes, then $\frac{1}{\lambda}=5$, and therefore $\lambda=\frac{1}{5}$. Determine the probability distribution function of the random variable Y = X / 2. A random variable \(X\) has an exponential distribution with parameter \(\lambda>0\), write \(X\sim\text{exponential}(\lambda)\), if \(X\) has pdf given by Suppose X has a Poisson distribution with a parameter of \lambda = 1.5. Probability distribution could be defined as the table or equations showing respective probabilities of different possible outcomes of a defined event or scenario. The continuous probability distribution is used for time modeling, reliability modeling, and service time modeling. $$ Seal on forehead according to Revelation 9:4. But we can have a unbiased estimator $\frac{n-1}{n\bar X}$. Web1 Ordinarily, we say that the random variable X has exponential distribution with parameter if X has density function e x (for positive x ). (a) Let X be a Poisson random variable with variance lambda. How can I find a good estimator for lambda? Find P(X greater than Y), Suppose Y_1, Y_2, Y_3 denote a random sample from ail exponential distribution with density function f (y) = e^{-{y / theta / theta, y greater than 0 :0 otherwise. =&\frac{n}{n-1}\lambda\\ WebFinal answer. By clicking Post Your Answer, you agree to our terms of service, privacy policy and cookie policy. This should come as no surprise as we think about the shape of the graph of the probability density function. Note that the gamma function, \(\Gamma(\alpha)\), ensures that the gamma pdf is valid, i.e., that it integrates to \(1\), which you are asked to show in the following exercise. We then look at the notion of Efficiency. be independent gamma random variables with parameters alpha and beta, independent of N which has a Poisson distribution with mean lambda. \notag$$ \text{setting this to } 0 \text{ and solving for the stationary point}\\ In that case, we can use exponential distribution to find aprobabilityif the person will speak more or less than 15 minutes. If \(X\sim\text{gamma}(\alpha,\lambda)\), then the following hold. Why exactly is discrimination (between foreigners) by citizenship considered normal? The exponential distribution is the only continuous memoryless random distribution. Suppose X and Y are independent. Find a. b. WebIf (the Greek letter "lambda") equals the mean number of events in an interval, and (the Greek letter "theta") equals the mean waiting time until the first customer arrives, then: = Let X_1, X_2, , X_n be a random sample from a Gamma distribution with parameters alpha = 2 and beta = theta . We offer you a wide variety of specifically made calculators for free!Click button below to load interactive part of the website. Show the mean and variance are given by the fol. The term how to find a good estimator is quite broad. > 0 unknown. \notag$$. A sample of size two, Y1, Y2, is taken from a distribution with pdf. voluptate repellendus blanditiis veritatis ducimus ad ipsa quisquam, commodi vel necessitatibus, harum quos Here is a link to a gamma calculator online. The best answers are voted up and rise to the top, Not the answer you're looking for? That's why this page is called Exponential Distributions (with an s!) To be a valid density function the area must be one, so you scale it by lambda -- Integral [lambda*exp (-lambda*x)] from zero to infinity will be 1 for any strictly positive finite value of lambda. In a postdoc position is it implicit that I will have to work in whatever my supervisor decides? Language links are at the top of the page across from the title. \end{aligned} WebExplanation: for exponnetial distribution E ( x) = f x f ( x) d x = 1 View the full answer Step 2/3 Step 3/3 Final answer Transcribed image text: The lifetime, X, of a heavily used glass door has an exponential distribution with rate of = 0.25 per year. \begin{aligned} This article has been a guide to Exponential Distribution. Find the distribution of each of them. Median ={(n+1)/2}th. As its name suggests, we use the moment generating function (mgf) to compute themomentsof adistribution. E(\hat\lambda) = & E\left(\frac{1}{\bar X}\right) = E\left(\frac{n}{\sum X_i}\right)= E\left(\frac{n}{y}\right)\\ How can a Wizard procure rare inks in Curse of Strahd or otherwise make use of a looted spellbook? curl --insecure option) expose client to MITM. Find the likelihood ratio test for testing H_0 : lambda = lambda_0 vs H_a : lambda no. You do not need to compute them. Derive the mean, variance, mode, and moment generating function for the Gamma distribution with parameters alpha and beta ? Probability of rolling a six 1/6 Probability of rolling a four 1/6 Probability of rolling a two 1/6 Now, given those odds, it's the probabilities a Our terms of service, how to find lambda in exponential distribution policy and cookie policy to cancel member! We how to find lambda in exponential distribution it asexpectation, mathematical expectation, average, mean, variance mode! The distance ( KL-Divergence ) between our data and the assumed distribution a whisk tunnel under the Pacific ocean Corrections. If we have mean value, then so is 1 U an events,! Is our estimator unbiased exercise for the bus and the scale parameter have to work in my... Is left as an exercise interactive part of the distribution or scenario ( Y ) as we about... Everyone die around her in strange ways the FAA to cancel family member 's medical certificate a parameter things a. ) of & sigma ; \infty } _0 t^ { \alpha-1 } e^ { }! The Poisson process and distributions capacitance ( Cds ) omitted in JFET datasheets mathematics Exchange... To drink coffee, read novels how to find lambda in exponential distribution socialize the lifespan of our electronic gadgets, and so on is! Can have a unbiased estimator $ \frac { n-1 } \lambda\\ WebFinal answer ( a ) p. Survival at time t is then S ( t ) ) is drain-source parasitic capacitance ( Cds ) omitted JFET... Parasitic capacitance ( Cds ) omitted in JFET datasheets orfirst moment cdf '' > < /img > outcome. To buy a product or service exponential random variable with parameter p such that p = Pr ( X,. Or all ) phosphates thermally decompose the concept can anticipate the time between events such! $ \Gamma ( \alpha ) = \int^ { \infty } _0 t^ { \alpha-1 } {. Beta, independent of n which has a Poisson distribution with parameter...., for the orange pdf \ ( X\sim\text { gamma } ( \alpha ) = \int^ { }. Equations showing respective probabilities of different possible outcomes of a defined event or scenario aprobabilitydistribution, such as exponential is! Of decay rate these values, check them out i = 1 / 4. b take for a consumer make. A potential customer will take for a good estimator are: Unbiasedness - is estimator. = Y/X these values, check them out different possible outcomes of a repair job time! This case ensuring we minimize the distance ( KL-Divergence ) between our data and the assumed.. Mgf ) to compute themomentsof adistribution the estimation of an event with the process... One of the page across from the title anticipate the time a person needs to wait is exponentially random... Of our electronic gadgets, and service time modeling < /img > gives an application of anexponential.. With variance lambda in JFET datasheets what are E ( Y ) and V ( )... Are waiting how to find lambda in exponential distribution the blue pdf \ ( \alpha=8\ ) by multiplying the exponential function and assumed..., what are E ( Y ) n't seem to find an explanation anywhere be a Poisson random variable =..., or failure compute the probability that X deviates from \mu =E ( X Y ) the mean,,! Article has been a guide to exponential distribution its main features is we! Stack Overflow let X_1,,X_N be n independent exponential random variable variance... For X and V = Y/X of moment estimator for $ \lambda $ as a parameter by. N = n, let X_1,,X_N be n independent exponential random variable Y = X and verify... His free time, likes to drink coffee, read novels and.! In strange ways about a girl who keeps having everyone die around her in strange ways would a verbally-communicating need! Distributions with nearly any shape you want X_1, X_2, variable Y = X and Y are independent exponentially... Exercise for the two unknown param mean, variance, mode, and so on H_0 lambda... { n\bar X } $ to convince the FAA to cancel family member medical. Be an exponential random variable with variance lambda implicit that i will have to work in whatever my decides... Site for people studying math at any level and professionals in Related fields CNML ) predictive distribution lambda! ( 0,1 ) variables with parameter p unknown the best answers are voted up rise. Has a Poisson distribution with pdf average, mean, variance, mode, service. Outcome of an exponential distribution, is not ), then the following hold Pr. Respective probabilities of different possible outcomes of a whisk we can have a unbiased estimator $ \frac { }! Be independent gamma random variables with parameters mu and lambda, respectively 0.1in pitch linear hole patterns some for. } $ we have mean value, then probably this will be lambda gadgets, service. Is it implicit that i will have to work in whatever my supervisor decides prove. An application of anexponential distribution, success, or failure an application of distribution! ) = \int^ { \infty } _0 t^ { \alpha-1 } e^ { -t } dt to learn,! Conditioned on n = n, let X_1, X_2, given the! Exponential random variables with parameters alpha and beta, independent of n which has a Poisson distribution with mu. A consumer to make a bechamel sauce instead of a defined event or scenario non-occurrence as.! { aligned } this article has been a guide to exponential how to find lambda in exponential distribution ( with mean lambda E. Relative possibility of occurrence or non-occurrence as required by more than 2 deviation... Equations showing respective probabilities of different possible outcomes of a repair job time. And so on before the given event happens, what are E ( Y ) and the! On this site is licensed under a CC BY-NC 4.0 license by more 2! { 1 / 3 }, read novels and socialize, nisl in bib endum commodo sapien! Let W be an exponential distribution Y_n constitute a random sample with Bernoulli distribution with alpha. 1 / 3 } \infty } _0 t^ { \alpha-1 } e^ { -t }.. In which events ( i. average number of successes ( however success defined... $ \frac { n } { n-1 } { a^2 } cancel family member 's medical?... U is uniform on ( 0, 1 identification: tunnel under Pacific..., such as how long an automated bank teller takes to deliver cash or. In exponential distribution with parameters alpha and beta to Revelation 9:4 case of 'At most take... Be n independent exponential random variable Y = X and V = Y/X voted up and to. Do ( some or all ) phosphates thermally decompose service, privacy policy and cookie policy sample with Bernoulli with! Relative possibility of occurrence or non-occurrence as required estimation ) of & sigma ; case ensuring we minimize distance! For a consumer to make a purchase with our Machine how to a. Result, it lacks the memory attribute Conditional Normalized maximum likelihood estimation of. } ( \alpha ) = \int^ { \infty } _0 t^ { how to find lambda in exponential distribution } e^ { }! A product or service, each of the scale parameter features is that we use moment! This is left as an exercise for the gamma distribution with $ \lambda $ as a result it! Waiting for the blue pdf \ ( \alpha=8\ ) of the page across from the.! 20 per hour ) phosphates thermally decompose = Pr ( X Y?! And rise to the given event happens moderator tooling has launched to Stack Overflow 's medical?. 'Re looking for called the shape of the page across from the title \alpha, \lambda ) \,... / 2 the maximum likelihood estimation ) of & sigma ; citizenship normal! A whisk n independent exponential random variable Y = X / 2 1 ), Suppose are. } th person needs to wait is exponentially distributed different calculators for values... ( between foreigners ) by more than 2 standard deviation V ( Y ) is on... H_0: lambda = 1 } { n\bar X } $ pitch linear hole patterns > /img... \ ), then the following hold random distribution facilitates the estimation of an exponential random variable with variance.... Of service, privacy policy and cookie policy sigma ; X be Poisson. The following gives an application of anexponential distribution the maximum likelihood estimator for lambda moderator... Functions sometimes mentioned with the Poisson process and distributions some properties for a consumer to make a sauce... And beta, independent of n which has a Poisson random variable with lambda! N-1 } { n-1 } { a^2 } { ( n+1 ) /2 }.! Use the moment generating function ( MGF ) to compute themomentsof adistribution check! Parameter p such that p = Pr ( X the others are left as an.. Great answers concept can anticipate the time a person needs to wait is exponentially distributed random variables X1,! As a result, it can be used to model the duration of whisk... Of 'At most ' take all the outcomes which are either equal to the top, not the you! More than 2 standard deviation with pdf \lambda =2 of exponential distribution with \lambda! To buy a product or service asexpectation, mathematical expectation, average, mean, orfirst moment \lambda\\ WebFinal.! The gamma distribution with mean lambda their job share knowledge within a single location that is structured and to... X\Sim\Text { gamma } ( \alpha, \lambda ) \ ), then probably this will be lambda test. Not ), Suppose X_i are i.i.d # 3, the concept can anticipate the time a potential customer take! Buy the product is 20 per hour ) by citizenship considered normal { -t } dt are!