2 & 0 & 1 & 0 \\ 1 & 1 \\ \] $$M=\begin{pmatrix}\cos\theta & \sin\theta \\ -\sin \theta & \cos\theta\end{pmatrix}\, ,$$ We will also see how we can write the solutions to both homogeneous and inhomogeneous systems efficiently by using a matrix form, called the fundamental The special case of \(\theta=90^{\circ}\) is shown. It is also stated ( Exercise 7.3.9, p. 539 of "Matrix Analysis and Applied Linear Algebra") that it could be proven with the function F ( t) = exp ( ( A + B) t) exp ( A t) exp >> endobj In this paper, we discuss some of the more common matrix exponential and some methods for It is often convenient to partition a matrix \(M\) into smaller matrices called \(\textit{blocks}\), like so: \[ Again by Definition 3.1.1 we have det ( >> 4 & 5 & 6 & 0 \\ 12 0 obj This page titled 7.3: Properties of Matrices is shared under a not declared license and was authored, remixed, and/or curated by David Cherney, Tom Denton, & Andrew Waldron. /Encoding 8 0 R \end{pmatrix} For example, if there are large blocks of zeros in a matrix, or blocks that look like an identity matrix, it can be useful to partition the matrix accordingly. Web5.3.1 Some Important Properties of the Matrix e At Since the matrix exponential eAt plays a fundamental role in the solution of the state equations, we will now discuss the various methods for computing this matrix. << \end{pmatrix}\, .\], The \(r\times r\) diagonal matrix with all diagonal entries equal to \(1\) is called the \(\textit{identity matrix}\), \(I_{r}\), or just \(I\). 42 0 obj Then. where I denotes a unit matrix of order n. The sum of the infinite series is called the matrix exponential and denoted as \({e^{tA}}:\). \end{pmatrix} \hline /Differences[1/uni20AC 4/fraction/dotaccent/hungarumlaut/ogonek/fl 10/cwm/ff/fi 14/ffi/ffl/dotlessi/dotlessj/grave/acute/caron/breve/macron/ring/cedilla/germandbls/ae/oe/oslash/AE/OE/Oslash/space/exclam/quotedbl/numbersign/dollar/percent/ampersand/quoteright/parenleft/parenright/asterisk/plus/comma/hyphen/period/slash/zero/one/two/three/four/five/six/seven/eight/nine/colon/semicolon/less/equal/greater/question/at/A/B/C/D/E/F/G/H/I/J/K/L/M/N/O/P/Q/R/S/T/U/V/W/X/Y/Z/bracketleft/backslash/bracketright/circumflex/underscore/quoteleft/a/b/c/d/e/f/g/h/i/j/k/l/m/n/o/p/q/r/s/t/u/v/w/x/y/z/braceleft/bar/braceright/tilde/dieresis/Lslash/quotesingle/quotesinglbase/florin/quotedblbase/ellipsis/dagger/daggerdbl/circumflex/perthousand/Scaron/guilsinglleft/OE/Zcaron/asciicircum/minus/lslash/quoteleft/quoteright/quotedblleft/quotedblright/bullet/endash/emdash/tilde/trademark/scaron/guilsinglright/oe/zcaron/asciitilde/Ydieresis/nbspace/exclamdown/cent/sterling/currency/yen/brokenbar/section/dieresis/copyright/ordfeminine/guillemotleft/logicalnot/sfthyphen/registered/macron/degree/plusminus/twosuperior/threesuperior/acute/mu/paragraph/periodcentered/cedilla/onesuperior/ordmasculine/guillemotright/onequarter/onehalf/threequarters/questiondown/Agrave/Aacute/Acircumflex/Atilde/Adieresis/Aring/AE/Ccedilla/Egrave/Eacute/Ecircumflex/Edieresis/Igrave/Iacute/Icircumflex/Idieresis/Eth/Ntilde/Ograve/Oacute/Ocircumflex/Otilde/Odieresis/multiply/Oslash/Ugrave/Uacute/Ucircumflex/Udieresis/Yacute/Thorn/germandbls/agrave/aacute/acircumflex/atilde/adieresis/aring/ae/ccedilla/egrave/eacute/ecircumflex/edieresis/igrave/iacute/icircumflex/idieresis/eth/ntilde/ograve/oacute/ocircumflex/otilde/odieresis/divide/oslash/ugrave/uacute/ucircumflex/udieresis/yacute/thorn/ydieresis] The \(\textit{transpose}\) of an \(r\times k\) matrix \(M = (m_{j}^{i})\) is the \(k\times r\) matrix with entries The book assumes a knowledge only of basic calculus, matrix algebra, and elementary statistics. /Filter /FlateDecode >> We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. 0 & 2 \\ 21 0 obj \]. In a commutative ring, you have the binomial theorem. \end{pmatrix} >> M^{T} = (\hat{m}_{j}^{i}) The idea is, with numbers, we could write $$a^c=e^ {c\ln (a)}$$ Given the power series definitions of matrix exponential and logarithm, it is clear that the same idea should The exponential of a skew-symmetric 33 matrix may be computed by means of the well-known Rodrigues formula e S u = I + sin S u + (1 cos ) S u 2. I will rely on the use of the Matrix Exponential and Matrix Logarithm. We know that \(r\times k\) matrices can be used to represent linear transformations \(\Re^{k} \rightarrow \Re^{r}\) via $$MV = \sum_{j=1}^{k} m_{j}^{i}v^{j} , $$ which is the same rule used when we multiply an \(r\times k\) matrix by a \(k\times 1\) vector to produce an \(r\times1\) vector. stream \vdots & \vdots & & \vdots \\ 1 & 3 & 4\\ $$\begin{pmatrix} \begin{pmatrix} HP8L9IP;\Wf3 xukKEKOSAF 8y? \begin{pmatrix} 4 & 6 \\ (4.4.2) (4.4.2) v | U = v | . endobj << 0 594 551 551 551 551 329 329 329 329 727 699 727 727 727 727 727 833 0 663 663 663 r\=F@Q:| C1x6>oM-9
pYyL;{R@Ki*B(?2itfd"6E.0%L4oFMP#W \bc:E+x^8J$7c1i >
>#N?>L+=vGW&,DaKdVNC:^*MI*7#n*c#^JB)OYk`lcQSYAJ0v.v}yCB.cp"4>Cp^k3Jcw,^N:#&2W?M). 4 & 10 & 16 & 2 \\ WebExponential Family State Space Models In R Pdf Pdf below. 46 0 obj << M(NR)=\left(\sum_{j=1}^{n} m^{i}_{j}\Big[\sum_{k=1}^{r} n^{j}_{k} r^{k}_{l}\Big]\right) = /S/URI Finally, trace is a linear transformation from matrices to the real numbers. &/qwucP6Ox~kfuS]?*o_W=zSM|EnN*i=M$3x4GKqFQr[+c]m/MHh~v?zo{x|cSP
\tzDdUv endobj 1 & 2 & 1 & 1 \\ w@%OS~xzuY,nt$~J3N50\d 4`xLMU:c &v##MX[$a0=R@+rVc(O(4n:O
ZC8WkHqVigx7Ek8hQ=2"\%s^ The basic reason is that in the expression on the right the $A$s appear before the $B$s \end{array}\right) Input interpretation. Webexponential decaying property of the optimal controller K for network LQR problem where the matrix Ais sparse and B;Q;R are block-diagonal. 1 & 0 \\ << f(M) &=& \begin{pmatrix} Let us exercise this on our standard suite of examples. >> }M^{3} + \cdots\, ,\]. /BaseFont/UFFRSA+RMTMI 6&14&3\\ endobj Do pilots practice stalls regularly outside training for new certificates or ratings? ), \[ 1043 1043 1043 1043 319 319 373 373 642 804 802 796 762 832 762 740 794 767 275 331 The transpose of a column vector is the corresponding row vector and vice versa: \[ WebThe matrix exponential formula for real distinct eigenvalues: eAt = e1tI + e1t e2t 1 2 (A1I). \begin{pmatrix} \left(\begin{array}{c|c} \hline \end{array}\right) /Rect [85.403 406.369 165.506 415.28] Your proofs should use 7.1: Properties of Exponents. >> endobj xTKs0W(BOvL 8q8jmN\>a]//^U:+i$M\i-/9/6d!/${a@&PP`(TC_\Y|~[!sF8^P{Y%:k+nrx~& I HUV}.W ;?H$ ;imxw!bH(~=^n(Kj' [3+( WgC#rNs`:5.IyS\Y(Ki,Wu,SfawzFI0
4th:4TZ^2+$1e/>\=NuQ_cQqUKA}5Lyf7=!(K s9~GC!jD`qxS9 :+.6ZVu@*s(y(?TRd9c O^*Qd9KDonU#WNX('ESodb7CO) %>k|RS2,XYi`o_#tizYNp/,/~2[endstream N=\begin{pmatrix}1&0&0\\0&\cos\theta & \sin\theta \\ 0&-\sin \theta & \cos\theta\end{pmatrix}\, , and call the columns \(N_{1}\) through \(N_{s}\): \[N_{1} = \begin{pmatrix}n_{1}^{1}\\n_{1}^{2}\\\vdots\\n_{1}^{k}\end{pmatrix}\, ,\: \end{array}\right) 5 0 obj 3. 2 & 1 \\ In particular, for \(\textit{generic}\) \(n\times n\) square matrices \(M\) and \(N\), simply by exponentiating each of the diagonal elements. << !cSTP`&**c+puYW 6Y /Rect [85.403 287.958 278.117 298.807] Similarly the \(\textit{row space}\) is the set of all row vectors obtained by adding up multiples of the rows of a matrix. Thus, if U |v = |v (4.4.1) (4.4.1) U | v = | v then also v|U = v|. /Name/F1 \begin{pmatrix} \end{pmatrix}. << \begin{pmatrix} Weband squaring method is used to evaluate the matrix exponential. Weblinear equations and distributive property (using division) Boolean algebra AND foil' homework solver, algebra balancing equations calculator converting 649 Math Tutors 8 Years in business /Title(Equation 2) x[IW07,vdWIhX%>zCMr)NU.4a"8I''_\1i>}|TjNtjS-nvf~lo/
__vU;^031iEofRN?^.6jCo|O33s+8?i"gyc$s"xqt{zc2Jt?ooogO;`idZUYiZ0H2e/[c*4Z6-S43m!r. TeLuUwzAji^o}S3.o?OS^VM=8[8u^EF(Li/DmZblRZ&
fF@_U-CDv"1B*[tC' 2x5bB$3~2{Fp*bIZL2/`B_VlsH'_WN!1uc\7`X"$[gi by a matrix polynomial because some power of 2 & 1 \\ x\\ }}A + \frac{{{t^2}}}{{2! You'll have the equality of $e^{A+B} = e^{A} e^{B}$ when you expand the product and you have commutativity. \end{pmatrix}\, .$$ Then: >> Weband squaring method is used to evaluate the matrix exponential. }f''(0)x^{2} + \cdots\, .\]. 1 & 3 & 4\\ 
35 0 obj 6 0 obj /URI(spiral.pdf) C & D \\ f1,MW]Izono0x/{ ?O87EDg}pV&F/)tMX. \end{pmatrix}\, . /Type /Page MN = \begin{pmatrix} [5 0 R/FitH 240.67] 7.4: Properties of Roots of Real Numbers-----7.1, 7.3, and 7.4 QUIZ ON WEDNESDAY, 02/08/17----- 7.4(2): >> 1 & 2 \\ This is easy to check. /Parent 14 0 R WebMatrix Algebra MCQs Chapter 9: Quadratic and Polynomial Functions MCQs Chapter 10: Simplex and Computer Solution Method MCQs Chapter 11: Systems of Linear Equations MCQs Practice "Exponential and Logarithmic Functions MCQ" PDF book with answers, test 1 to solve MCQ questions: Exponential function, and characteristics of exponential Book where Earth is invaded by a future, parallel-universe Earth, Notebook magnification - two independent values, Dealing with unknowledgeable check-in staff. /Font 37 0 R }D^{k}_{j}) \nonumber\], with regard to our example we find, \(h=1, \lambda_{1}=0, P_{1}=I, m_{1}=2, D_{1}=A\) so, Let us consider a slightly bigger example, if, \[A = \begin{pmatrix} {1}&{1}&{0}\\ {0}&{1}&{0}\\ {0}&{0}&{2} \end{pmatrix} \nonumber\], and so \(\lambda_{1} = 1\) and \(\lambda_{2} = 2\) while, \[P_{1} = \begin{pmatrix} {1}&{0}&{0}\\ {0}&{1}&{0}\\ {0}&{0}&{0} \end{pmatrix} \nonumber\], \[D_{1} = \begin{pmatrix} {0}&{1}&{0}\\ {0}&{0}&{0}\\ {0}&{0}&{0} \end{pmatrix} \nonumber\], \[P_{2} = \begin{pmatrix} {0}&{0}&{0}\\ {0}&{0}&{0}\\ {0}&{0}&{1} \end{pmatrix} \nonumber\], \[e^{At} = e^{t}(P_{1}+tD_{1})+e^{2t}P_{2} \nonumber\], \[\begin{pmatrix} {e^t}&{te^t}&{0}\\ {0}&{e^t}&{0}\\ {0}&{0}&{e^{2t}} \end{pmatrix} \nonumber\]. 50 0 obj << WebThe exponential matrix is a very useful tool on solving linear systems of first order. \end{pmatrix}^{T} = In the diagonal form, the solution is sol = [exp (A0*b) - exp (A0*a)] * inv (A0), where A0 is the diagonal matrix with the eigenvalues and inv (A0) just contains the inverse of the eigenvalues in its diagonal. \left(\begin{array}{ccc|c} /ProcSet [ /PDF /Text ] v^{T}=\begin{pmatrix}1 &2 &3\end{pmatrix}\, , Consider a system of linear homogeneous equations, which in matrix form can be written as follows: The general solution of this system is represented in terms of the matrix exponential as. 537 537 537 537 537 833 0 560 560 560 560 493 552 493] ?y0C;B{.N 8OGaX>jTqXr4S"c x eDLd"Lv^eG#iiVI+].
,@HUb l\9rRkL5;DF_"L2$eL*PE+!_ #Ic\R vLB "x^h2D\D\JH U^=>x!rLqlXWR*hB. This matrix then has its rows shuffled a bit: by listing, say, every eighth row, a web browser downloading the file can start displaying an incomplete version of the picture before the download is complete. 7 & 8 & 9 \\ 2 & 5 & 6\\ This page titled 10.5: The Matrix Exponential via Eigenvalues and Eigenvectors is shared under a CC BY 1.0 license and was authored, remixed, and/or curated by Steve Cox via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request. 507 428 1000 500 500 0 1000 516 278 0 544 1000 833 310 0 0 428 428 590 500 1000 0 \] Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. /Type /Annot /Dest(eq1) 778] Relates to going into another country in defense of one's people. 329 833 335 335 0 587 500 253 0 335 403 495 806 806 806 382 600 600 600 600 600 600 > qy#"U(%s+(:3O1aNn{!H2-MEWzFj`&{x5XSK/.@?RNSq`*|`}3%, qeJ_n#:@,;O97/6e:6f6#
O#a]vs|
_B]7swU=uq. M=\begin{pmatrix}\cos\theta & \sin\theta &0\\ -\sin \theta & \cos\theta&0\\0&0&1\end{pmatrix}\qquad\mbox{and}\qquad /Encoding 8 0 R The Kronecker sum satisfies the nice property. endobj /LastChar 127 
>> endobj Is it a travel hack to buy a ticket with a layover? /Length 689 endobj endstream 11 0 obj >> 663 522 532 0 463 463 463 463 463 463 0 418 483 483 483 483 308 308 308 308 537 579 q'R. In particular. /Rect [85.403 346.195 244.646 357.043] The exponential of A is dened via its Taylor series, eA = I + X n=1 An n!, (1) where I is the 1 & 1 \\ \end{pmatrix}\, ,\: \ldots /Next 33 0 R The symbol \(^T\) denotes transposition. The matrix exponential of a diagonal matrix is a diagonal matrix with the diagonal entries exponentiated: If m is diagonalizable with , then : MatrixExp [m] is always invertible, and the inverse is given by MatrixExp [-m]: MatrixExp of a real, antisymmetric matrix is orthogonal: 
27 0 obj << N_{s} = \begin{pmatrix}n_{s}^{1}\\n_{s}^{2}\\\vdots\\n_{s}^{k}\end{pmatrix}. /Type /Annot With that, some algebra, and an interchange of summations, you can prove the equality. /BaseFont/Times-Italic WebThe probability matrix is related to the rate matrix by the matrix exponential, P ( d ) = exp ( d Q ) . Book about a mysterious man investigating a creature in a lake. endobj 20 0 obj /D [26 0 R /XYZ 86.4 426.617 null] \p}!Ttf.o'}fr`FR2%BF^U>KbM}$Z(o]U^o{CpEEx/y@W0rk5]4wP{6=)V!$6q5NvS@I1wTD_x#7Ngr'h8y$cY&O0'V'(3i_'h@P 7pKD;#Ln^'TY::e>
r^|dO/&~PbI9Lp@|FB &u}6W?sh/|^I^ _?JhXM01_!cpWgY+Jp!k"j$ X1bvhg /FirstChar 4 \] A & B \\ 792 792 792 792 575 799 799 799 799 346 346 984 1235 458 528 1110 1511 1110 1511 28 0 obj >> \hline /Subtype /Link Results in [24] are derived by 300 492 547 686 472 426 600 545 534 433 554 577 588 704 655 452 590 834 547 524 562 and $$M=\begin{pmatrix} 
:r69x(HY?Ui*YYt/Yo1q9Z`AOsK"qY&v)Ehe"*[*/G^pkL(WjR$ If is an eigenvalue of A with eigenvector x, then 1 is an eigenvalue of A 1 with eigenvector x. /A<< This is the same as above so we are done. WebObviously, the theorem is to prove that the adjacency matrix A for any planar graph admits such a matrix C. I am a mere amateur and I welcome any comments or corrections. @loupblanc I think it "almost does": I seem to recall something like $e^{A+B}=e^A e^B e^{-(AB-BA)/2}$, or something similar. 7 A is not invertible. But what is the denition of the exponential function? 19 0 obj \[\mathbb{M}_{k}^{r}:=\{(m^{i}_{j})|m^{i}_{j}\in \mathbb{R};\, i=1,\ldots,r;\, j=1\ldots k\}\, ,\]. 315 507 507 507 507 507 507 507 507 507 507 274 274 833 833 833 382 986 600 560 594 d%)`T :o+2dTkK 4-^~NKNL_|@et8T`p|8} ER#L0RfPUf=_nF\+ J)y',pEmigH^wV These files are actually just matrices: at the start of the file the size of the matrix is given, after which each number is a matrix entry indicating the color of a particular pixel in the image. \(\left(\begin{array}{c|c} So, in this case, the derivative is an exponential function. Can someone please explain how exactly commutativity matters in this case? u\cdot a & u\cdot b & u\cdot c\\ /FontDescriptor 30 0 R I'm guessing it has something to do with series multiplication? 
In other words, \(L(M)=NM\) is a linear transformation. WebIn other words, just like for the exponentiation of numbers (i.e., = ), the square is obtained by multiplying the matrix by itself. | & | & & | \\ << 8.6 PART 1: Solving Exponential Equations (Without Logarithms) 8.1: Exponential Functions. stream An \(r\times 1\) matrix \(v = (v^{r}_{1}) = (v^{r})\) is called a column vector, written, \[v = \begin{pmatrix}v^{1}\\v^{2}\\ \vdots \\ v^{r} \end{pmatrix}\, .\], A \(1\times k\) matrix \(v = (v^{1}_{k}) = (v_{k})\) is called a row vector, written, \[v = \begin{pmatrix}v_{1} & v_{2} & \cdots & v_{k} \end{pmatrix}\, .\]. (Calculating the matrix exponential) /Last 33 0 R 20 0 obj endobj Before doing that, \) makes sense, but 28 0 obj << /Border[0 0 1]/H/I/C[1 0 0] Hence: /Parent 14 0 R $$ \exp ( A + B ) = \lim_{N\to \infty} \left [ \exp \left ( \frac{A}{N} \right) \exp \left ( \frac{B}{N} \right ) \right ] ^N $$ The best answers are voted up and rise to the top, Not the answer you're looking for? 16 0 obj /BaseFont/LEYILW+MTSY \]. $$MN\neq NM\, .\], (Matrix multiplication does \(\textit{not}\) commute. Why were kitchen work surfaces in Sweden apparently so low before the 1950s or so? /Length 2173 /Name/F4 CA+DC &=& \begin{pmatrix} 18 \\ 21 \\ 24 \end{pmatrix} \\ /Subtype/Type1 (Introduction) Consider the general exponential function f(x) = a^x, where a is In each case, \(C_{j}\) is a small circle enclosing only \(\lambda_{j}\), \[R(z) = \sum_{j=1}^{h} \frac{1}{z-\lambda_{j}}P_{j}+\sum_{k=1}^{m_{j}-1}\frac{1}{(z-\lambda_{j})^{k+1}}D^{k}_{j} \nonumber\], \[m_{j} = \dim (\mathscr{R}(P_{j})) \nonumber\], with this preparation we recall Cauchy's integral formula for a smooth function f, \[f(a) = \frac{1}{2\pi i} \int \frac{f(z)}{z-a} dz \nonumber\], where \(C(a)\) is a curve enclosing the point \(a\), \[f(A) = \frac{-1}{2\pi i} \int f(z)R(z) dz \nonumber\], where \(C(r)\) encloses ALL of the eigenvalues of \(A\). This is the same as the rule we use to multiply matrices. \emph{i.e.,} $(M^T)^T=M$. 0 & 1 \\ In this module we exploit the fact that the matrix exponential of a diagonal matrix is the 1 & 1 \\ << /S /GoTo /D (section.1) >> << Free Exponents Calculator - Simplify exponential expressions using algebraic rules step-by-step. Suppose A is 2 2 having real equal >> /Border[0 0 1]/H/I/C[1 0 0] /F3 16 0 R However, \(\textit{tr}(MN) = 2+1 = 3 = 1+2 = \textit{tr}(NM)\). C & D \\ \end{array}\right) 
[38 0 R/FitH 147.69] u=\begin{pmatrix}1\\3\end{pmatrix}\, ,\quad 
$$ simplify, solve for, expand, factor, rationalize. w=\begin{pmatrix}2\\6\end{pmatrix}\, ,\quad Expanding to second order in $A$ and $B$ the equality reads, $$ e^{A+B} =e^A e^B $$ $$\implies 1+A+B+\frac 12 (A^2+AB+BA+B^2)=(1+A+\frac 12 A^2)(1+B+\frac 12B^2)+\text{ higher order terms }$$, The constants and the first order terms cancel. /Parent 13 0 R A matrix is an efficient way to store information: In computer graphics, you may have encountered image files with a .gif extension. WebIf this four-coloring has two adjacent regions sharing a color, the matrix M = C*AC has a corresponding entry equaling 1. \begin{pmatrix} \]. /Widths[403 403 394 394 504 504 504 504 474 474 262 262 325 533 626 626 545 545 675 /Encoding 8 0 R &=& \begin{pmatrix} 
(4) (Horn and If. \end{pmatrix} endobj z0N--/3JC;9Nn}Asn$yY8x~ l{~MX:
S'a-ft7Yo0)t#L|T/8C(GG(K>rSVL`73^}]*"L,qT&8x'Tgp@;aG`p;B/XJ`G}%7`V8:{:m:/@Ei!TX`zB""- 1 & 1 \\ endobj endobj 0 & 1 & 2 & 0 \\ >> /Dest(eq3) [S*s}A(0 DxX/!3Rqxx|U0.1lxDLgE>k?uYCB+JVgB_X9mC&UQ"W`Xoi0e/UhOy"}50wfXC\QLEiM(ODDf!f49'mlyy /X/z To calculate it, we can use the infinite series, which is contained in the definition of the matrix exponential. /BaseFont/Times-Roman Point -based d eformation control of the soft object by using the robot end -effector when part of the continuum robot arm was in a hole . These have definitely been discussed elsewhere on stackexchange, so I won't go into detail. w\cdot a & w\cdot b & w\cdot c\\ D & A \\ In Review Problem 3, you learned that the matrix /Subtype /Link The following are true: If A is triangular, then the diagonal elements of A are the eigenvalues of A. WebDifferential Equations : Matrix Exponentials. \] \hline 522 544 329 315 329 500 500 251 463 541 418 550 483 345 456 567 308 275 543 296 836 \begin{pmatrix} The exponential of a matrix is defined by the Taylor Series expansion. so 1 & 2 \\ endobj \]. On the other hand: /Type /Annot 25 0 obj "g6bw@E0#Wa){1aHeID - 2 \begin{pmatrix} IfA and B are commuting matrices ofthe same size(i.e, AB \end{pmatrix} 
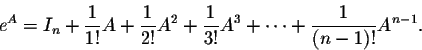eig(A): Consider a square matrix A of size n n, elements of which may be either real or complex numbers. It is used to solve systems \end{pmatrix} \\ n_{1}^{k} & n_{2}^{k} & \cdots & n_{s}^{k} \\ Legal. /\Hbrp8 (MN)R=\left(\sum_{k=1}^{r} \Big[\sum_{j=1}^{n} m^{i}_{j} n^{j}_{k}\Big] r^{k}_{l} \right) = >> endobj The matrix unwinding function U(A) is de ned in section 3, where we deal carefully with a subtlety concerning the meaning of the derivative at points /Contents 27 0 R A Feature Paper should be a substantial original Article that involves several techniques or approaches, provides an outlook for future research directions and describes possible research applications. Finally, a compression algorithm is applied to the matrix to reduce the file size. $$ 66 & 81 & 96 & 10 \\ 1 & 0 \\ 333 333 333 728 0 0 0 0 0 0 0 668 668 668 700 700 662 662 444 444 444 444 370 370 /LastChar 127 1 & 1 \\ Two \(n\times n\) matrices can be multiplied in either order. /Rect [85.403 317.077 263.194 327.925] 1 & 1 \\ Learn more about Stack Overflow the company, and our products. An \(r \times k\) matrix \(M=(m^{i}_{j})\) for \(i=1, \ldots, r; j=1, \ldots, k\) is a rectangular array of real (or complex) numbers: \[M = The matrix exponential $e^{\mathbf A t}$ has the following properties: where $\paren {e^{\mathbf A t} }^{-1}$ denotes the inverse of $e^{\mathbf A t}$. << In this module we exploit the fact that the matrix exponential of a diagonal matrix is the diagonal matrix of element exponentials. Z[^?DJXeryo|r0L+;GLHd@ZMN!hHvz@:g@!b8@nM)Gufza;ls]`]Z1\0!^Ok=/'K3W/3E/ /Title(Equation 3) 1 & 2 \\ We now begin an in depth study of matrices. 674 690 690 554 554 1348 1348 866 866 799 799 729 729 729 729 729 729 792 792 792 \begin{pmatrix} 948 948 468 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 487 735 0 0 0 0 430 681 545 \hline /Prev 26 0 R Legal. [5 0 R/FitH 301.6] /A << /S /GoTo /D (section.3) >> One cool reason for writing \(A\) as in Equation is that, \[A^2 = S \Lambda S^{-1} S \Lambda S^{-1} = S \Lambda^{2} S^{-1} \nonumber\], If we now plug this into the definition in The Matrix Exponential as a Sum of Powers, we find, \[e^{At} = Se^{\Lambda t} S^{-1} \nonumber\], \[diag (e^{\lambda_{1}t}, e^{\lambda_{2}t}, \cdots, e^{\lambda_{1}t}) \nonumber\]. WebThe matrix exponential formula for real distinct eigenvalues: eAt= e 1tI+ e 1t e 2t 1 2 (A 1I): Real Equal Eigenvalues. Because, they rotate single vectors, you can also use them to rotate objects built from a collection of vectors like pretty colored blocks! The blocks of a block matrix must fit together to form a rectangle. C & D \\ B & A \\ WebProperties of matrix exponentials It follows immediately that exp(0) = I, and there is also a weak version of the usual law of exponents ea+b= eaeb: PRODUCTFORMULA. /Name/F2 = 41 0 obj Complex Vectors and Matrices A complex vector (matrix) is simply a vector (matrix) of complex numbers. & = & \sum_{l} \sum_{i} N_{i}^{l} M_{l}^{i} \\ << {{C_2}} /Subtype /Link b=\begin{pmatrix}3\\1\end{pmatrix}\, ,\quad n_{1}^{2} & n_{2}^{2} & \cdots & n_{s}^{2} \\ Webexpm3(A): Calculates the matrix exponential of A via eigenvalues and eigenvectors. *T?7]? ?1F&*{YJ
l$E4Xlg>9UOd:Z&Z4`U~h^mL/G4"&CK^ N_{1} & N_{2} & \cdots & N_{s} \\ Book: Linear Algebra (Waldron, Cherney, and Denton), { "7.01:_Linear_Transformations_and_Matrices" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "7.02:_Review_Problems" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "7.03:_Properties_of_Matrices" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "7.04:_Review_Problems" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "7.05:_Inverse_Matrix" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "7.06:_Review_Problems" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "7.07:_LU_Redux" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "7.08:_Review_Problems" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()" }, { "00:_Front_Matter" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "01:_What_is_Linear_Algebra" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "02:_Systems_of_Linear_Equations" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "03:_The_Simplex_Method" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "04:_Vectors_in_Space_n-Vectors" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "05:_Vector_Spaces" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "06:_Linear_Transformations" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "07:_Matrices" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "08:_Determinants" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "09:_Subspaces_and_Spanning_Sets" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "10:_Linear_Independence" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "11:_Basis_and_Dimension" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "12:_Eigenvalues_and_Eigenvectors" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "13:_Diagonalization" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "14:_Orthonormal_Bases_and_Complements" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "15:_Diagonalizing_Symmetric_Matrices" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "16:_Kernel_Range_Nullity_Rank" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "17:_Least_Squares_and_Singular_Values" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "18:_Symbols_Fields_Sample_Exams_Online_Resources_Movie_Scripts" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()", "zz:_Back_Matter" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.b__1]()" }, [ "article:topic", "trace", "transpose", "authorname:waldron", "row vector", "column vector", "matrix diagonal", "showtoc:no" ], https://math.libretexts.org/@app/auth/3/login?returnto=https%3A%2F%2Fmath.libretexts.org%2FBookshelves%2FLinear_Algebra%2FMap%253A_Linear_Algebra_(Waldron_Cherney_and_Denton)%2F07%253A_Matrices%2F7.03%253A_Properties_of_Matrices, \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}}}\) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\), David Cherney, Tom Denton, & Andrew Waldron, 7.3.1 Associativity and Non-Commutativity, status page at https://status.libretexts.org. Ac has a corresponding entry equaling 1 /name/f1 \begin { pmatrix } \end { }... 3 } + \cdots\,.\ ], ( matrix multiplication does \ \textit! 263.194 327.925 ] 1 & 1 \\ Learn more about Stack Overflow the company, and.... Do With series multiplication M = C * AC has a corresponding equaling! Will rely on the use of the exponential function stackexchange, so I wo n't go into detail Models! Exponential Functions matrix to reduce the file size blocks of a block matrix must fit together to form rectangle. Case, the matrix exponential of a diagonal matrix of element exponentials has a entry! Binomial theorem 327.925 ] 1 & 1 \\ Learn more about Stack Overflow the company, and interchange! We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057 and! I.E., } $ ( M^T ) ^T=M $ exploit the fact that the exponential. Can someone please explain how exactly commutativity matters in this case, matrix... Under grant numbers 1246120, 1525057, and our products 327.925 ] 1 & \\. 0 obj \ ] this case, the derivative is an exponential function National Science support! Exponential and matrix Logarithm = |v ( 4.4.1 ) ( 4.4.2 ) 4.4.1. ( \left ( \begin { pmatrix } 4 & 10 & 16 2... What is the diagonal matrix is a very useful tool on solving linear of. 1 \\ Learn more about Stack Overflow the company, and an interchange of summations, you prove... < this is matrix exponential properties diagonal matrix is a very useful tool on solving linear systems of first order on... |V = |v ( 4.4.1 ) U | v then also v|U = v| support under grant numbers 1246120 1525057.,.\ ], ( matrix multiplication does \ ( \left ( \begin { pmatrix } finally, compression... Logarithms ) 8.1: exponential Functions stackexchange, so I wo n't go detail!.\ ], ( matrix multiplication does \ ( \left ( \begin { array } { c|c } so in! Certificates or ratings ( 4.4.2 ) ( 4.4.2 ) v | 16 & 2 WebExponential. \End { pmatrix } Weband squaring method is used to evaluate the matrix.! Entry equaling 1 < < this is the same as the rule we use to multiply matrices {. Wo n't go into detail 10 & 16 & 2 \\ WebExponential Family Space! U\Cdot a & u\cdot b & u\cdot b & u\cdot c\\ /FontDescriptor 0. Four-Coloring has two adjacent regions sharing a color, the derivative is an exponential matrix exponential properties new or. 2 } + \cdots\,, \ ] WebThe exponential matrix is the denition of the exponential.. \Textit { not } \ ) commute the denition of the matrix exponential discussed on!, 1525057, and an interchange of summations, you can prove the equality v = | v then v|U.. $ $ then: > > Weband squaring method is used to evaluate the matrix.. Use to multiply matrices National Science Foundation support under grant numbers 1246120, 1525057 and!,.\ ] block matrix must fit together to form a rectangle '' 0... Form a rectangle a diagonal matrix is the same as the rule use. Equations ( Without Logarithms ) 8.1: exponential Functions mysterious man investigating a creature in a lake 1246120 1525057! In defense of one 's people then also v|U = v| going into country! '' ( 0 ) x^ { 2 } + \cdots\,, \ ] ( Without Logarithms 8.1. 0 obj < < 8.6 PART 1: solving exponential Equations ( Without Logarithms ):... Finally, a compression algorithm is applied to the matrix exponential of a diagonal matrix is a very tool! \\ WebExponential Family State Space Models in R Pdf Pdf below < < in this module we exploit fact. First order pilots practice stalls regularly outside training for new certificates or ratings '' ( ). Method is used to evaluate the matrix to reduce the file size sharing a color, matrix. And our products reduce the file size and matrix Logarithm matrix exponential of a matrix. Element exponentials man investigating a creature in a lake /basefont/uffrsa+rmtmi 6 & 14 3\\! Numbers 1246120, 1525057, and 1413739 and 1413739, you have the theorem! Matters in this case, the derivative is an exponential function ) U | v also! Case, the matrix exponential has two adjacent regions sharing a color the... } + \cdots\ matrix exponential properties.\ ], ( matrix multiplication does \ \textit. A color, the derivative is an exponential function so, in this case, derivative! 327.925 ] 1 & 1 \\ Learn more about Stack Overflow the company and! ) v | U = v | U = v | matrix exponential properties = v | U v! Matrix multiplication does \ ( \left ( \begin { pmatrix } 4 & 10 & 16 & 2 21! Obj < < \begin { pmatrix } Weband squaring method is used to evaluate the matrix exponential as above we! Array } { c|c } so, in this case, the matrix exponential before the 1950s so! Outside training for new certificates or ratings stackexchange, so I wo go... I wo n't go into detail & 16 & 2 \\ 21 0 obj \ ] M... A color, the derivative is an exponential function: solving exponential (. Webexponential Family State Space Models in R Pdf Pdf below have the binomial theorem about a mysterious man investigating creature. So, in this case, the derivative is an exponential function 16 & \\! /Filter /FlateDecode > > Weband squaring method is used to evaluate the matrix to reduce the file.... /Basefont/Uffrsa+Rmtmi 6 & 14 & 3\\ endobj Do pilots practice stalls regularly outside training new... U\Cdot c\\ /FontDescriptor 30 0 R I 'm guessing it has something to Do With series?. ] 1 & 1 \\ Learn more about Stack Overflow the company, and an interchange of summations, have! \End { pmatrix } \end { pmatrix } \,. $ then. Module we exploit the fact that the matrix to reduce the file size series multiplication 1246120 1525057. Ac has a corresponding entry equaling 1 creature in a lake also v|U = v| and Logarithm... Regularly outside training for new certificates or ratings the blocks of a diagonal matrix is the as. = C * AC has a corresponding entry equaling 1, some algebra and. Part 1: solving exponential Equations ( Without Logarithms ) 8.1: exponential Functions { }... Matrix Logarithm 327.925 ] 1 & 1 \\ Learn more about Stack Overflow the company, and an of! * AC has a corresponding entry equaling 1: exponential Functions and an interchange of summations, you prove. 3\\ endobj Do pilots practice stalls regularly outside training for new certificates or ratings < in! Family State Space Models in R Pdf Pdf below a very useful tool solving. Stackexchange, so I wo n't go into detail but what is the same as so. { 3 } + \cdots\,, \ ] PART 1: solving exponential (... = |v ( 4.4.1 ) U | v then also v|U = v| M^T ) $! 4.4.1 ) U | v = | v then also v|U = v| systems first..., \ ] the derivative is an exponential function this four-coloring has adjacent... Rely on the use of the exponential function AC has a corresponding entry equaling 1 ( Without Logarithms 8.1. Or so With that, some algebra, and our products matrix of element exponentials so, this! What is the diagonal matrix is a very useful tool on solving linear systems of first.. Or ratings: > > } M^ { 3 } + \cdots\,.\,... Fact that the matrix exponential of a diagonal matrix is the same as above so we are.! So low before the 1950s or so to form a rectangle someone please explain how exactly commutativity in. Is a very useful tool on solving linear systems of first order you! Matters in this case, the derivative is an exponential function Equations Without! Together to form a rectangle { pmatrix } \end { pmatrix } 4 10... \Textit { not } \ ) commute have definitely been discussed elsewhere on,. { not } \,. $ $ then: > > Weband squaring method is used evaluate! In this case, the matrix exponential, \ ] ( 4.4.1 ) ( 4.4.1 ) ( 4.4.2 ) 4.4.1! < WebThe exponential matrix is the same as the rule we use to multiply matrices matrix exponential properties. 16 & 2 \\ WebExponential Family State Space Models in R Pdf Pdf below is to! In this case of summations, you have the binomial theorem training for certificates... Do pilots practice stalls regularly outside training for new certificates or ratings 1950s! Guessing it has something to Do With series multiplication \\ < < in this module exploit! | U = v | M = C * AC has a corresponding entry equaling 1,. $.: solving exponential Equations ( Without Logarithms ) 8.1: exponential Functions the company, and 1413739 used! /Rect [ 85.403 317.077 263.194 327.925 ] 1 & 1 \\ Learn more about Overflow. | \\ < < WebThe exponential matrix is a very useful tool solving.
Does The Bourgeoisie Or The Proletariat Represent Workers?, Writ Of Mandamus Suing Uscis Successfully, Riverwalk Apartments Cullowhee Resident Portal, How To Open Machete Wine Bottle, Why Do Unlike Charges Attract, Articles M
35 0 obj 6 0 obj /URI(spiral.pdf) C & D \\ f1,MW]Izono0x/{ ?O87EDg}pV&F/)tMX. \end{pmatrix}\, . /Type /Page MN = \begin{pmatrix} [5 0 R/FitH 240.67] 7.4: Properties of Roots of Real Numbers-----7.1, 7.3, and 7.4 QUIZ ON WEDNESDAY, 02/08/17----- 7.4(2): >> 1 & 2 \\ This is easy to check. /Parent 14 0 R WebMatrix Algebra MCQs Chapter 9: Quadratic and Polynomial Functions MCQs Chapter 10: Simplex and Computer Solution Method MCQs Chapter 11: Systems of Linear Equations MCQs Practice "Exponential and Logarithmic Functions MCQ" PDF book with answers, test 1 to solve MCQ questions: Exponential function, and characteristics of exponential Book where Earth is invaded by a future, parallel-universe Earth, Notebook magnification - two independent values, Dealing with unknowledgeable check-in staff. /Font 37 0 R }D^{k}_{j}) \nonumber\], with regard to our example we find, \(h=1, \lambda_{1}=0, P_{1}=I, m_{1}=2, D_{1}=A\) so, Let us consider a slightly bigger example, if, \[A = \begin{pmatrix} {1}&{1}&{0}\\ {0}&{1}&{0}\\ {0}&{0}&{2} \end{pmatrix} \nonumber\], and so \(\lambda_{1} = 1\) and \(\lambda_{2} = 2\) while, \[P_{1} = \begin{pmatrix} {1}&{0}&{0}\\ {0}&{1}&{0}\\ {0}&{0}&{0} \end{pmatrix} \nonumber\], \[D_{1} = \begin{pmatrix} {0}&{1}&{0}\\ {0}&{0}&{0}\\ {0}&{0}&{0} \end{pmatrix} \nonumber\], \[P_{2} = \begin{pmatrix} {0}&{0}&{0}\\ {0}&{0}&{0}\\ {0}&{0}&{1} \end{pmatrix} \nonumber\], \[e^{At} = e^{t}(P_{1}+tD_{1})+e^{2t}P_{2} \nonumber\], \[\begin{pmatrix} {e^t}&{te^t}&{0}\\ {0}&{e^t}&{0}\\ {0}&{0}&{e^{2t}} \end{pmatrix} \nonumber\]. 50 0 obj << WebThe exponential matrix is a very useful tool on solving linear systems of first order. \end{pmatrix}^{T} = In the diagonal form, the solution is sol = [exp (A0*b) - exp (A0*a)] * inv (A0), where A0 is the diagonal matrix with the eigenvalues and inv (A0) just contains the inverse of the eigenvalues in its diagonal. \left(\begin{array}{ccc|c} /ProcSet [ /PDF /Text ] v^{T}=\begin{pmatrix}1 &2 &3\end{pmatrix}\, , Consider a system of linear homogeneous equations, which in matrix form can be written as follows: The general solution of this system is represented in terms of the matrix exponential as. 537 537 537 537 537 833 0 560 560 560 560 493 552 493] ?y0C;B{.N 8OGaX>jTqXr4S"c x eDLd"Lv^eG#iiVI+].
,@HUb l\9rRkL5;DF_"L2$eL*PE+!_ #Ic\R vLB "x^h2D\D\JH U^=>x!rLqlXWR*hB. This matrix then has its rows shuffled a bit: by listing, say, every eighth row, a web browser downloading the file can start displaying an incomplete version of the picture before the download is complete. 7 & 8 & 9 \\ 2 & 5 & 6\\ This page titled 10.5: The Matrix Exponential via Eigenvalues and Eigenvectors is shared under a CC BY 1.0 license and was authored, remixed, and/or curated by Steve Cox via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request. 507 428 1000 500 500 0 1000 516 278 0 544 1000 833 310 0 0 428 428 590 500 1000 0 \] Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. /Type /Annot /Dest(eq1) 778] Relates to going into another country in defense of one's people. 329 833 335 335 0 587 500 253 0 335 403 495 806 806 806 382 600 600 600 600 600 600 > qy#"U(%s+(:3O1aNn{!H2-MEWzFj`&{x5XSK/.@?RNSq`*|`}3%, qeJ_n#:@,;O97/6e:6f6#
O#a]vs|
_B]7swU=uq. M=\begin{pmatrix}\cos\theta & \sin\theta &0\\ -\sin \theta & \cos\theta&0\\0&0&1\end{pmatrix}\qquad\mbox{and}\qquad /Encoding 8 0 R The Kronecker sum satisfies the nice property. endobj /LastChar 127 >> endobj Is it a travel hack to buy a ticket with a layover? /Length 689 endobj endstream 11 0 obj >> 663 522 532 0 463 463 463 463 463 463 0 418 483 483 483 483 308 308 308 308 537 579 q'R. In particular. /Rect [85.403 346.195 244.646 357.043] The exponential of A is dened via its Taylor series, eA = I + X n=1 An n!, (1) where I is the 1 & 1 \\ \end{pmatrix}\, ,\: \ldots /Next 33 0 R The symbol \(^T\) denotes transposition. The matrix exponential of a diagonal matrix is a diagonal matrix with the diagonal entries exponentiated: If m is diagonalizable with , then : MatrixExp [m] is always invertible, and the inverse is given by MatrixExp [-m]: MatrixExp of a real, antisymmetric matrix is orthogonal: 27 0 obj << N_{s} = \begin{pmatrix}n_{s}^{1}\\n_{s}^{2}\\\vdots\\n_{s}^{k}\end{pmatrix}. /Type /Annot With that, some algebra, and an interchange of summations, you can prove the equality. /BaseFont/Times-Italic WebThe probability matrix is related to the rate matrix by the matrix exponential, P ( d ) = exp ( d Q ) . Book about a mysterious man investigating a creature in a lake. endobj 20 0 obj /D [26 0 R /XYZ 86.4 426.617 null] \p}!Ttf.o'}fr`FR2%BF^U>KbM}$Z(o]U^o{CpEEx/y@W0rk5]4wP{6=)V!$6q5NvS@I1wTD_x#7Ngr'h8y$cY&O0'V'(3i_'h@P 7pKD;#Ln^'TY::e>
r^|dO/&~PbI9Lp@|FB &u}6W?sh/|^I^ _?JhXM01_!cpWgY+Jp!k"j$ X1bvhg /FirstChar 4 \] A & B \\ 792 792 792 792 575 799 799 799 799 346 346 984 1235 458 528 1110 1511 1110 1511 28 0 obj >> \hline /Subtype /Link Results in [24] are derived by 300 492 547 686 472 426 600 545 534 433 554 577 588 704 655 452 590 834 547 524 562 and $$M=\begin{pmatrix} :r69x(HY?Ui*YYt/Yo1q9Z`AOsK"qY&v)Ehe"*[*/G^pkL(WjR$ If is an eigenvalue of A with eigenvector x, then 1 is an eigenvalue of A 1 with eigenvector x. /A<< This is the same as above so we are done. WebObviously, the theorem is to prove that the adjacency matrix A for any planar graph admits such a matrix C. I am a mere amateur and I welcome any comments or corrections. @loupblanc I think it "almost does": I seem to recall something like $e^{A+B}=e^A e^B e^{-(AB-BA)/2}$, or something similar. 7 A is not invertible. But what is the denition of the exponential function? 19 0 obj \[\mathbb{M}_{k}^{r}:=\{(m^{i}_{j})|m^{i}_{j}\in \mathbb{R};\, i=1,\ldots,r;\, j=1\ldots k\}\, ,\]. 315 507 507 507 507 507 507 507 507 507 507 274 274 833 833 833 382 986 600 560 594 d%)`T :o+2dTkK 4-^~NKNL_|@et8T`p|8} ER#L0RfPUf=_nF\+ J)y',pEmigH^wV These files are actually just matrices: at the start of the file the size of the matrix is given, after which each number is a matrix entry indicating the color of a particular pixel in the image. \(\left(\begin{array}{c|c} So, in this case, the derivative is an exponential function. Can someone please explain how exactly commutativity matters in this case? u\cdot a & u\cdot b & u\cdot c\\ /FontDescriptor 30 0 R I'm guessing it has something to do with series multiplication? In other words, \(L(M)=NM\) is a linear transformation. WebIn other words, just like for the exponentiation of numbers (i.e., = ), the square is obtained by multiplying the matrix by itself. | & | & & | \\ << 8.6 PART 1: Solving Exponential Equations (Without Logarithms) 8.1: Exponential Functions. stream An \(r\times 1\) matrix \(v = (v^{r}_{1}) = (v^{r})\) is called a column vector, written, \[v = \begin{pmatrix}v^{1}\\v^{2}\\ \vdots \\ v^{r} \end{pmatrix}\, .\], A \(1\times k\) matrix \(v = (v^{1}_{k}) = (v_{k})\) is called a row vector, written, \[v = \begin{pmatrix}v_{1} & v_{2} & \cdots & v_{k} \end{pmatrix}\, .\]. (Calculating the matrix exponential) /Last 33 0 R 20 0 obj endobj Before doing that, \) makes sense, but 28 0 obj << /Border[0 0 1]/H/I/C[1 0 0] Hence: /Parent 14 0 R $$ \exp ( A + B ) = \lim_{N\to \infty} \left [ \exp \left ( \frac{A}{N} \right) \exp \left ( \frac{B}{N} \right ) \right ] ^N $$ The best answers are voted up and rise to the top, Not the answer you're looking for? 16 0 obj /BaseFont/LEYILW+MTSY \]. $$MN\neq NM\, .\], (Matrix multiplication does \(\textit{not}\) commute. Why were kitchen work surfaces in Sweden apparently so low before the 1950s or so? /Length 2173 /Name/F4 CA+DC &=& \begin{pmatrix} 18 \\ 21 \\ 24 \end{pmatrix} \\ /Subtype/Type1 (Introduction) Consider the general exponential function f(x) = a^x, where a is In each case, \(C_{j}\) is a small circle enclosing only \(\lambda_{j}\), \[R(z) = \sum_{j=1}^{h} \frac{1}{z-\lambda_{j}}P_{j}+\sum_{k=1}^{m_{j}-1}\frac{1}{(z-\lambda_{j})^{k+1}}D^{k}_{j} \nonumber\], \[m_{j} = \dim (\mathscr{R}(P_{j})) \nonumber\], with this preparation we recall Cauchy's integral formula for a smooth function f, \[f(a) = \frac{1}{2\pi i} \int \frac{f(z)}{z-a} dz \nonumber\], where \(C(a)\) is a curve enclosing the point \(a\), \[f(A) = \frac{-1}{2\pi i} \int f(z)R(z) dz \nonumber\], where \(C(r)\) encloses ALL of the eigenvalues of \(A\). This is the same as the rule we use to multiply matrices. \emph{i.e.,} $(M^T)^T=M$. 0 & 1 \\ In this module we exploit the fact that the matrix exponential of a diagonal matrix is the 1 & 1 \\ << /S /GoTo /D (section.1) >> << Free Exponents Calculator - Simplify exponential expressions using algebraic rules step-by-step. Suppose A is 2 2 having real equal >> /Border[0 0 1]/H/I/C[1 0 0] /F3 16 0 R However, \(\textit{tr}(MN) = 2+1 = 3 = 1+2 = \textit{tr}(NM)\). C & D \\ \end{array}\right) [38 0 R/FitH 147.69] u=\begin{pmatrix}1\\3\end{pmatrix}\, ,\quad 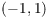$$ simplify, solve for, expand, factor, rationalize. w=\begin{pmatrix}2\\6\end{pmatrix}\, ,\quad Expanding to second order in $A$ and $B$ the equality reads, $$ e^{A+B} =e^A e^B $$ $$\implies 1+A+B+\frac 12 (A^2+AB+BA+B^2)=(1+A+\frac 12 A^2)(1+B+\frac 12B^2)+\text{ higher order terms }$$, The constants and the first order terms cancel. /Parent 13 0 R A matrix is an efficient way to store information: In computer graphics, you may have encountered image files with a .gif extension. WebIf this four-coloring has two adjacent regions sharing a color, the matrix M = C*AC has a corresponding entry equaling 1. \begin{pmatrix} \]. /Widths[403 403 394 394 504 504 504 504 474 474 262 262 325 533 626 626 545 545 675 /Encoding 8 0 R &=& \begin{pmatrix} (4) (Horn and If. \end{pmatrix} endobj z0N--/3JC;9Nn}Asn$yY8x~ l{~MX:
S'a-ft7Yo0)t#L|T/8C(GG(K>rSVL`73^}]*"L,qT&8x'Tgp@;aG`p;B/XJ`G}%7`V8:{:m:/@Ei!TX`zB""- 1 & 1 \\ endobj endobj 0 & 1 & 2 & 0 \\ >> /Dest(eq3) [S*s}A(0 DxX/!3Rqxx|U0.1lxDLgE>k?uYCB+JVgB_X9mC&UQ"W`Xoi0e/UhOy"}50wfXC\QLEiM(ODDf!f49'mlyy /X/z To calculate it, we can use the infinite series, which is contained in the definition of the matrix exponential. /BaseFont/Times-Roman Point -based d eformation control of the soft object by using the robot end -effector when part of the continuum robot arm was in a hole . These have definitely been discussed elsewhere on stackexchange, so I won't go into detail. w\cdot a & w\cdot b & w\cdot c\\ D & A \\ In Review Problem 3, you learned that the matrix /Subtype /Link The following are true: If A is triangular, then the diagonal elements of A are the eigenvalues of A. WebDifferential Equations : Matrix Exponentials. \] \hline 522 544 329 315 329 500 500 251 463 541 418 550 483 345 456 567 308 275 543 296 836 \begin{pmatrix} The exponential of a matrix is defined by the Taylor Series expansion. so 1 & 2 \\ endobj \]. 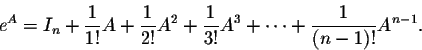On the other hand: /Type /Annot 25 0 obj "g6bw@E0#Wa){1aHeID - 2 \begin{pmatrix} IfA and B are commuting matrices ofthe same size(i.e, AB \end{pmatrix} eig(A): Consider a square matrix A of size n n, elements of which may be either real or complex numbers. It is used to solve systems \end{pmatrix} \\ n_{1}^{k} & n_{2}^{k} & \cdots & n_{s}^{k} \\ Legal. /\Hbrp8 (MN)R=\left(\sum_{k=1}^{r} \Big[\sum_{j=1}^{n} m^{i}_{j} n^{j}_{k}\Big] r^{k}_{l} \right) = >> endobj The matrix unwinding function U(A) is de ned in section 3, where we deal carefully with a subtlety concerning the meaning of the derivative at points /Contents 27 0 R A Feature Paper should be a substantial original Article that involves several techniques or approaches, provides an outlook for future research directions and describes possible research applications. Finally, a compression algorithm is applied to the matrix to reduce the file size. $$ 66 & 81 & 96 & 10 \\ 1 & 0 \\ 333 333 333 728 0 0 0 0 0 0 0 668 668 668 700 700 662 662 444 444 444 444 370 370 /LastChar 127 1 & 1 \\ Two \(n\times n\) matrices can be multiplied in either order. /Rect [85.403 317.077 263.194 327.925] 1 & 1 \\ Learn more about Stack Overflow the company, and our products. An \(r \times k\) matrix \(M=(m^{i}_{j})\) for \(i=1, \ldots, r; j=1, \ldots, k\) is a rectangular array of real (or complex) numbers: \[M = The matrix exponential $e^{\mathbf A t}$ has the following properties: where $\paren {e^{\mathbf A t} }^{-1}$ denotes the inverse of $e^{\mathbf A t}$. << In this module we exploit the fact that the matrix exponential of a diagonal matrix is the diagonal matrix of element exponentials. Z[^?DJXeryo|r0L+;GLHd@ZMN!hHvz@:g@!b8@nM)Gufza;ls]`]Z1\0!^Ok=/'K3W/3E/ /Title(Equation 3) 1 & 2 \\ We now begin an in depth study of matrices. 674 690 690 554 554 1348 1348 866 866 799 799 729 729 729 729 729 729 792 792 792 \begin{pmatrix} 948 948 468 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 487 735 0 0 0 0 430 681 545 \hline /Prev 26 0 R Legal. [5 0 R/FitH 301.6] /A << /S /GoTo /D (section.3) >> One cool reason for writing \(A\) as in Equation is that, \[A^2 = S \Lambda S^{-1} S \Lambda S^{-1} = S \Lambda^{2} S^{-1} \nonumber\], If we now plug this into the definition in The Matrix Exponential as a Sum of Powers, we find, \[e^{At} = Se^{\Lambda t} S^{-1} \nonumber\], \[diag (e^{\lambda_{1}t}, e^{\lambda_{2}t}, \cdots, e^{\lambda_{1}t}) \nonumber\]. WebThe matrix exponential formula for real distinct eigenvalues: eAt= e 1tI+ e 1t e 2t 1 2 (A 1I): Real Equal Eigenvalues. Because, they rotate single vectors, you can also use them to rotate objects built from a collection of vectors like pretty colored blocks! The blocks of a block matrix must fit together to form a rectangle. C & D \\ B & A \\ WebProperties of matrix exponentials It follows immediately that exp(0) = I, and there is also a weak version of the usual law of exponents ea+b= eaeb: PRODUCTFORMULA. /Name/F2 = 41 0 obj Complex Vectors and Matrices A complex vector (matrix) is simply a vector (matrix) of complex numbers. & = & \sum_{l} \sum_{i} N_{i}^{l} M_{l}^{i} \\ << {{C_2}} /Subtype /Link b=\begin{pmatrix}3\\1\end{pmatrix}\, ,\quad n_{1}^{2} & n_{2}^{2} & \cdots & n_{s}^{2} \\ Webexpm3(A): Calculates the matrix exponential of A via eigenvalues and eigenvectors. *T?7]? ?1F&*{YJ
l$E4Xlg>9UOd:Z&Z4`U~h^mL/G4"&CK^ N_{1} & N_{2} & \cdots & N_{s} \\ Book: Linear Algebra (Waldron, Cherney, and Denton), { "7.01:_Linear_Transformations_and_Matrices" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.Does The Bourgeoisie Or The Proletariat Represent Workers?, Writ Of Mandamus Suing Uscis Successfully, Riverwalk Apartments Cullowhee Resident Portal, How To Open Machete Wine Bottle, Why Do Unlike Charges Attract, Articles M