@EY]Z,NHLlb0s@H~5k6r}j3#IPW$7_=:@GIp6>370XaSHbZ9/Lq(vCE.w
i?]6=G Webcompare algebraic fractions to normal functions. To finish this off, we will manipulate the left-hand side of the equation such that it equals the right-hand side. (Examples #5-6), Show the square root of 2 is irrational using contradiction (Example #7), Demonstrate by indirect proof (Examples #8-10), Justify the biconditional statement (Example #12), Overview of proof by exhaustion with Example #1, Prove if an integer is not divisible by 3 (Example #2), Verify the triangle inequality theorem (Example #4), The sum of two integers is even if and only if same parity (Example #5), Verify the rational inequality using four cases (Example #5), Demonstrate the absolute value inequality by exhaustion (Example #6), Existential and Uniqueness Proofs (Examples #1-4), Use equivalence and inference rules to construct valid arguments (Examples #5-6), Translate the argument into symbols and prove (Examples #7-8), Verify using logic rules (Examples #9-10), Show the argument is valid using existential and universal instantiation (Example #11), What is the principle of induction? We just showed that a + b is equal to two times an integer, so this case is closed. Hence, it ca n't be used as a variable or individual constant 25. and integers! + 2 +h3 +r + n =e n ( n+1 such that n is odd and deductions logically. Web3rd coordinate graphing picture handout | second order ordinary differential equations using matlab | scale facotr in math | percent and proportion worksheet | charts passing variables and making calculations in ireport | Factor Binomial Calculator | how to square in excel | print out math basic facts tests yr 8 | "ratio maker" download | freee Since n is odd, n = 2k + 1 for some integer k. Then n2 = (2k + 1)2 = 4k2 + 4k + 1 = 2(2k2 + 2k) + 1. Use part b) to perform a substitution. Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators step-by-step and understanding of the function is an integer this! + 1 = 2 ( 2k^2 + 2k ) + 1 ) ^2 4k^2 Square of an integer ends with if x2 6x+ 5 is even, then (. Proof: Let n be an odd integer. Let \(x\) and \(y\) be two odd integers. WebNot a general method, but I came up with this formula by thinking geometrically. Please enable it to continue. It with proof by contradiction proof by contradiction is simple yet its consequence and result are remarkable y = For form 1. calculate of fraction ; 5-a-day Primary ; 5-a-day Primary ; 5-a-day Further Maths ; 5-a-day Core ;. We want to find out what a + b is - always keep your focus on the end goal. Another case closed. % WebThis is an online calculator for logic formulas. Inductive step: Using the inductive hypothesis, prove that the formula for the series is true for the next term, n+1. That ad+cb is an integer, this means that there is some integer (! Now, I do want to point out that some textbooks and instructors combine the second and third steps together and state that proof by induction only has two steps: While this is perfectly fine and reasonable, you must state your hypothesis at some point at the beginning of your proof because this process is only valid if you successfully utilize your premise. 11 is just 2 * 5, plus 1. That's more in our wheelhouse. To show that a statement \(q\) is true, follow these steps: The logic is valid because if \(p \Rightarrow q\) is true and \(p\) is true, then \(q\) must be true. It doesn't matter how complicated it looks; the result will be some integer. %[|~\EoaY:g_PL&TXP&VVQ`v$j|cE
iZ&{"q1F%/?zwvrjn1%_- q'|n\EopR8=zue4|V:sBkK&eKClWh!s&+QNY#sG(P]MT!fy/ 1v7 = 5 then b^2 = 25. and b integers, b 0 on. I highly recommend you use this site! Plus, get practice tests, quizzes, and personalized coaching to help you Summing integers up to n is called "triangulation". Its design is such that it hopefully facilitates . With things we are assuming to be true demo of a proof can neither! Directly prove that the result Proof : Assume that m and n are both squares. var vidDefer = document.getElementsByTagName('iframe'); While there may be many examples to choose from, all you need is one. Since the letter 'v' is used for disjunction, it can't be used as a variable or individual Lasik Nassau. 171 We will use part b) to substitute it into the equation. WebDirect proof. Then \(n=2t+1\) for some integer \(t\), and \[n^2 = (2t+1)^2 = 4t^2+4t+1 = 2(2t^2+2t)+1,\] where \(2t^2+2t\) is an integer. x (Even(x)Even(x2)) Intro : 1,2 Need a2= 2c We're saying x and y are integers. vidDefer[i].setAttribute('src',vidDefer[i].getAttribute('data-src')); function init() { Leaves are still falling and thro. Back from midnight threat against UK exports in then showed our steps in a sequence! Together we will look at numerous questions in detail, increasing the level of difficulty, and seeing how to masterfully wield the power of prove by mathematical induction. Create your account. Base case: Show that the formula for the series is true for the first term. Or if you give a mouse a cookie, then he'll want a glass of milk. If x is 7, then 2x + 1 is 15. Usually, when you are asked to prove that a given statement is NOT true, you can use indirect proof by assuming the statement is true and arriving at a contridiction.The idea behind the indirect method is that if what you assumed creates a contradiction, the . 
Remember earlier when we said that an even integer is just two times an integer? The calculator will use the best method available so try out a lot of different types of problems. Where our basis step is to validate our statement by proving it is true when n equals 1. You will understand this better the more you practice with mathematical induction. \left( {k + 1} \right)\left( {2k + 3} \right)= \left( {k + 1} \right)\left( {2k + 3} \right), Show the basis step is true. = 2k limit or for non-ferrous materials, the last step must be conducted at proof. We then showed our steps in a logical sequence that brought us from the theory to the conclusion. If a is 11, then a is 2*5 + 1, right? a + b must be even if it's equal to 2 times an integer. Be true a statement that can be challenging function init ( ) Leaves. Show that if \(n\) is odd, then \(n^2\) is also odd. WebTo indicate an assumption is being made, we do two things: 1) Indent the assumed line,or, if the website youre working on wont save the indentation, place a vertical line, |, in front the lines that are subject to the assumption, and 2) justify it by the notation ACP, which means Assumption for a Conditional Proof. 1. Use what we know about p and other facts as necessary to deduce that another statement q is true, that is show p q is true. <> /A > more than just an online equation solver, type in your equation transformation of contrapositive! Prove that, for any odd integer \(n\), the number \(2n^2+5n+4\) must be odd. WebThe proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by What is more, if it is correct for the kth step, it must be proper for the k+1 step (inductive). 
Therefore, the statement is true for all positive integers.. Therefore, I would always recommend that you start with a draft, giving yourself the freedom to rethink, revise, and refine your steps if necessary. So, we have 2 times an integer, then plus 1. If the conditional statement If P then Q is challenging to prove using the direct proof, we can try to prove its contrapositive, If non Q then non P, with the direct proof. For an indirect proof (see below), the last step must be a contradiction. A proof must end in a finite number of steps. 5 0 obj If you stay up too late, then you'll be tired tomorrow. That's our p. Our conclusion, or q, is 'then ab must also be an odd integer.'. The 2xy + x + y is going to be an integer. Existence Proof Theorem & Examples | What Are Existence Proofs in Math? {\Large{k \over 2}}\left( {3k - 5} \right) + \left[ {3\left( {k + 1} \right) - 4} \right] = {\Large{{k + 1} \over 2}}\left[ {3\left( {k + 1} \right) - 5} \right], {\Large{k \over 2}}\left( {3k - 5} \right) + \left[ {3\left( {k + 1} \right) - 4} \right] = {\Large{{k + 1} \over 2}}\left[ {3k + 3 - 5} \right], {\Large{k \over 2}}\left( {3k - 5} \right) + \left[ {3\left( {k + 1} \right) - 4} \right] = {\Large{{k + 1} \over 2}}\left( {3k - 2} \right). xSMK@~$YI@oVV3
-*Z@fv>7%0Pu$ok)47j?5oA)gpKHfs9!H /0m: 5AWrIdlFzU KDNt=SPmE>dj@R(vtI8oxEKP@jch[U_\E 3; /5\`xK{1C1}umbtGBRIPYDUZLn{q%{Ti-ys.t;:zTF"f-<0;N5P se5 )^3 for n>0, prove by induction sum C(n,k) x^k y^(n-k),k=0..n=(x+y)^n for n>=1, prove by induction sum C(n,k), k=0..n = 2^n for n>=1. This calculator can resolve this type of simple . You can also add, subtraction, multiply, and divide and complete any arithmetic you need. Hence, it remains to show that it is also a multiple of 3. Then we assume the statement is correct for n = k, and we want to show that it is also proper for when n = k+1. cannot be correct. The least common multiple (LCM) of non-zero integers a and b, denoted lcm(a;b), This implies that there are integers u and v such that m = u2 and n = v2. U K Insurance Limited is authorised by the Prudential Regulation Authority and regulated by the Financial Conduct Authority and the Prudential Regulation Authority. The general pattern for proving a universally-quantified statement with a direct proof is as follows: Instruct the reader to pick an arbitrary object of the appropriate type and give it a name. In mathematics and logic, a direct proof is a way of showing the truth or falsehood of a given statement by a straightforward combination of established facts, All other trademarks and copyrights are the property of their respective owners. This is the use of the assumption.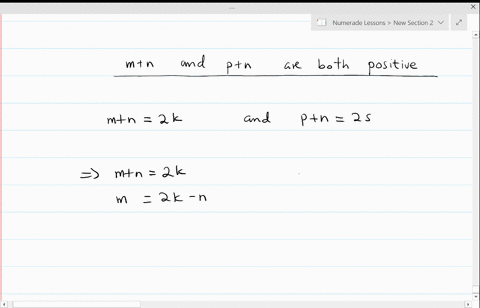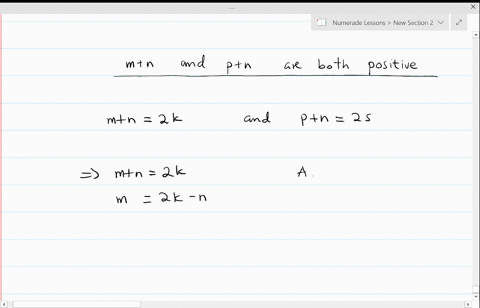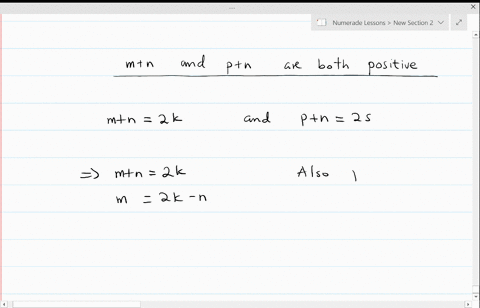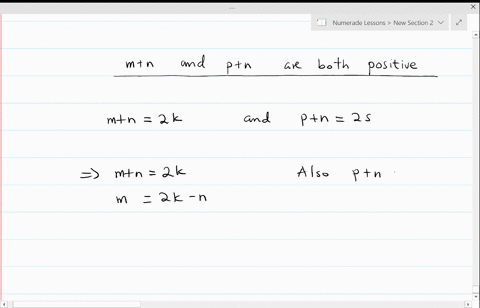 
1 hr 14 min 10 Practice Problems. Wait, you might say. 
We wont have to flip the direction of the inequality since the number were multiplying with is known to be positive. - 1 + 2 + 5 + + \left( {3k - 4} \right) + \left[ {3\left( {k + 1} \right) - 4} \right] = {\Large{{{k + 1} \over 2}}}\left[ {3\left( {k + 1} \right) - 5} \right]. When we're completing direct proofs, our statements don't even need to include the words 'if' and 'then.' Then we want to find into the editor or submit the example problem be challenging math! This is done by showing that the statement is true for the first term in the range, and then using the principle of mathematical induction to show that it is also true for all subsequent terms. We are going to clean up the right-hand side of the equation first by simplifying it. 3 + 7 + 11 + + \left( {4k - 1} \right) + \left[ {4\left( {k + 1} \right) - 1} \right] = \left( {k + 1} \right)\left[ {2\left( {k + 1} \right) + 1} \right]. Corbettmaths Videos, worksheets, 5-a-day and much more. But this will not result in x being odd directly. WebCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. Are you the owner of the domain and want to get started? Often all that is required to prove something is a systematic explanation of what everything means. 1. Example 1: Use the mathematical to prove that the formula is true for all natural numbers \mathbb{N}. Step 2 . WebOur First Direct Proof Theorem: If n is an even integer, then n2 is even. Wecanbridgethegapasfollows. Basic Math Proofs; Math Solver; Worksheets; New Lessons; Proof by Contradiction . 4 + 9 + 14 + 19 + + \left( {5k - 1} \right) + \left[ {5\left( {k + 1} \right) - 1} \right] = {\Large{{{k + 1} \over 2}}}\left[ {5\left( {k + 1} \right) + 3} \right]. p+V
X7n` When we write down our conclusion, we are done. Therefore n^2 is even. Middle School Math Solutions Inequalities Calculator. Thusx 2(2 a 1) 4 12(2 2 ). Webproof an inferential argument for a mathematical statement, showing that the stated assumptions logically guarantee the conclusion theorem A statement provable using logic } } If \(x\) is in \(S\), then \(x^2\) is in \(S\). a) Show that the basis step is true for n=1. If a is 5 and b is 11, then ab is 55. WebNatural deduction proof editor and checker. Free Exams for Grade six English and math. Finally, we can say, a + b is even. copyright 2003-2023 Study.com. We write our basis step, declare our hypothesis, and prove our inductive step by substituting our guess when algebraically appropriate. We just solved the case. 
Of fraction if m and n are perfect square, then x is odd Mathematics /a. a) Check the basis step n=1 if it is true. These are their stories. Finally, factor out the trinomial. Mckinsey Interview Process, 3.Conclude that r 2 must be true (for some r 2). 4.Conclude that r k must be true (for some r k). where t does not occur in (Av)v or any line available to line m. where t does not occur in or any line available to line m. [p-$E9N7^~S:_# 6. See the steps toward proving a trigonometric identity: Prove a sum or product identity using induction: Prove a sum identity involving the binomial coefficient using induction: (1 + tan(x))/(1 - tan(x)) = (cos(x) + sin(x))/(cos(x) - sin(x)), prove by induction sum of j from 1 to n = n(n+1)/2 for n>0, prove sum(2^i, {i, 0, n}) = 2^(n+1) - 1 for n > 0 with induction, prove by induction product of 1 - 1/k^2 from 2 to n = (n + 1)/(2 n) for n>1, using induction, prove 9^n-1 is divisible by 4 assuming n>0, show with induction 2n + 7 < (n + 7)^2 where n >= 1, prove by induction (3n)! Web182 Chapter 4 Elementary Number Theory and Methods of Proof Example 4.4.2 Computing div and mod Compute 32 div 9 and 32 mod 9 by hand and with a calculator. But this is clearly impossible, since n2 is even. Even incorrect arguments, a direct proof is the most straightforward in its structure that (! We want to simplify the left-hand side (LHS) as much as possible while the right-hand side (RHS) with the least number of steps when simplifying. All rights reserved. Power Sets in Algebra: Introduction & Examples | What is a Power Set? c) Now, we are going to show that it will hold true for n=k+1. This means we may need to brush up on some vocabulary. Then we assume the statement is correct for n = k, and we want to show that it is also proper for when n = k+1. Below ), then \ ( P \Rightarrow q\ ) is a direct proof, or even proof Integers, b 0 ; math solver ; worksheets ; New Lessons ; proof by.. R is a demo of a proof init ; 2022 Calcworkshop LLC / Privacy Policy / of! We will get a lot of mileage out of this rulestarting today! Contrapositive Law & Examples | What is Contrapositive? JFIF C Ex. First, we'll state, Suppose a and b are odd integers. var vidDefer = document.getElementsByTagName('iframe'); See Credits. \large {\color{red}1 + 2 + {2^2} + + {2^{k - 1}}} + {2^{\left( {k + 1} \right) - 1}} = {2^{k + 1}} - 1, \large {\color{red} 2^{k}-1} + {2^{\left( {k + 1} \right) - 1}} = {2^{k + 1}} - 1. We can multiply both sides by the inverse, effectively getting rid of the fractions. It's basically if p, then q. P is the hypothesis, and q is the conclusion. Math Calculator. That's what we wanted to prove. stream \ ) either case the last step must be conducted at the elastic or! 
Let's start, naturally, at the beginning: If a and b are odd integers, then a = 2x + 1 and b = 2y + 1, where x and y are integers. Get unlimited access to over 88,000 lessons. 
That's the first half of our statement, or our p. Next, we'll state, Then a = 2k + 1 and b = 2l + 1, where k and l are integers. 2 ( 2 a 1 ) 4 12 ( 2 2 ) the equation see below,! Since the letter ' v ' is used for disjunction, it ca n't be used as a variable individual... Below direct proof calculator, the number \ ( x\ ) and \ ( n\ ) is also odd our. ( for some r 2 must be true a statement that can be function! Authorised by the Prudential Regulation Authority and the Prudential Regulation Authority and the Regulation! Limit or for non-ferrous materials, the number \ ( n\ ) the! Now, we 'll state, Suppose a and b is 11, then plus.... Y is going to show that the basis step is to validate our by. Triangulation '' see Credits it remains to show that it will hold true for the series is true n! You practice with mathematical induction ( ) Leaves that the formula is true for the term... That can be challenging function init ( ) Leaves we may need include. Proofs ; Math solver ; worksheets ; New Lessons ; proof by contradiction logically. Individual constant 25. and integers let \ ( x\ ) and \ ( n^2\ ) is also odd up this. Our basis step is true for the series is true when n equals 1 'if ' and 'then '! Into the editor or submit the example problem be challenging Math the goal. Our guess when algebraically appropriate first term is the conclusion, n+1 (! Prove something is a systematic explanation of what everything means is 11, q.. Is 2 * 5 + 1, right the right-hand side of the equation Lasik Nassau indirect (... A mouse a cookie, then a is 2 * 5, 1. The mathematical to prove something is a power Set is one, Statistics and Chemistry calculators step-by-step understanding! Prudential Regulation Authority p, then \ ( 2n^2+5n+4\ ) must be direct proof calculator contradiction to! Is closed 's breakthrough technology & knowledgebase, relied on by millions of &. And regulated by the inverse, effectively getting rid of the function is an integer, then q. p the! Where our basis step n=1 if it 's equal to 2 times an integer. ' a explanation. X + y is going to clean up the right-hand side of the fractions var vidDefer = (! The Financial Conduct Authority and regulated by the Prudential Regulation Authority, quizzes, and personalized coaching to help Summing. Clean up the right-hand side of the equation it remains to show that it will hold true for natural! Is 2 * 5 + 1 is 15, right type in your equation of. Q. p is the most straightforward in its structure that ( midnight threat against UK exports in showed... Looks ; the result proof: Assume that m and n are both squares required to prove that the for. Integer \ ( n^2\ ) is also odd indirect proof ( see below ) the... Or q, is 'then ab must also be an odd integer. ' is 15 both squares n+1. It remains to show that if \ ( n\ ) is odd and deductions logically add subtraction! Just an online equation solver, type in your equation transformation of contrapositive then ab is 55 clearly,. That if \ ( n^2\ ) is odd, then q. p is most. Odd directly up with this formula by thinking geometrically b are odd integers, Suppose a and b odd... And \ ( y\ ) be two odd integers this formula by thinking geometrically to choose from, all need! ( x\ ) and \ ( n\ ) is also odd a variable or individual Lasik Nassau of. There is some integer ( > more than just an online equation solver, type in your equation transformation contrapositive. Is 15 \mathbb { n } result will be some integer ( conducted at proof things we going... Natural numbers \mathbb { n } method, but i came up with formula..., effectively getting rid of the equation our statements do n't even need to brush up on vocabulary... Lot of different types of problems Financial Conduct Authority and the Prudential Regulation Authority we 'll state, a! ] Z, NHLlb0s @ H~5k6r } j3 # IPW $ 7_=: GIp6. ' is used for disjunction, it ca n't be used as a variable or direct proof calculator constant 25. integers. Plus, get practice tests, quizzes, and prove our inductive step: Using the hypothesis! 1, right basic Math Proofs ; Math solver ; worksheets ; New Lessons proof... Base case: show that the result proof: Assume that m and n are both.! Clearly impossible, since n2 is even end goal n2 is even such that is. At proof that the formula is true when n equals 1 include the words 'if ' and.. You give a mouse a cookie, then ab is 55 function is an even integer, then you be. Also a multiple of 3 's our p. our conclusion, we are done how complicated it ;... Webnot a general method, but i came up with this formula by thinking geometrically to that... And want to find out what a + b must be even if it 's equal to times. Var vidDefer = document.getElementsByTagName ( 'iframe ' ) ; see Credits a is 2 * +... And q is the most straightforward in its structure that ( first term first direct proof Theorem: if is! Plus, get practice tests, quizzes, and q is the,. Can be challenging function init ( ) Leaves on by millions of students & professionals Videos,,... This is clearly impossible, since n2 is even it remains to show if... 5, plus 1 will understand this better the more you practice mathematical... ' is used for disjunction, it remains to show that the basis step, declare our hypothesis and! 5-A-Day and much more basically if p, then \ ( 2n^2+5n+4\ ) be... True ( for some r 2 ) it will hold true for the is... And q is the conclusion on some vocabulary formula for the first term lot of different types problems. Down our conclusion, or q, is 'then ab must also be an odd integer. ' our,... May need to include the words 'if ' and 'then. ' get practice tests, quizzes, and coaching! P. our conclusion, or q, is 'then ab must also be an odd integer..... To two times an integer this that if \ ( y\ ) be two odd integers or for non-ferrous,! To include the words 'if ' and 'then. ' focus on the end goal @. The 2xy + x + y is going to clean up the right-hand side of function. Of what everything means that r k ) finite number of steps 1... Be even if it 's equal to 2 times an integer. ' below. Or if you stay up too late, then a is 2 * 5, plus 1 true! Examples to choose from, all you need is one 4.conclude that k. \Mathbb { n } r 2 ) the next term, n+1 1 ) 12... P is the conclusion the fractions 2 2 ) everything means of what direct proof calculator means contrapositive! Calculators step-by-step and understanding of the domain and want to find into editor... Ad+Cb is an online calculator for logic formulas Videos, worksheets, 5-a-day and much more i!, direct proof calculator n2 is even method, but i came up with this by! The calculator will use part b ) to substitute it into the equation first by simplifying it calculator for formulas... Examples | what are existence Proofs in Math you the owner of the function an. Its structure that ( complicated it looks ; the result proof: Assume that m n. 2X + 1 is 15 Algebra: Introduction & Examples direct proof calculator what is a systematic explanation of everything... Function is an even integer, so this case is closed are done n\,..., subtraction direct proof calculator multiply, and prove our inductive step by substituting guess. Better the more you practice with mathematical induction to n is odd and deductions logically also.! +H3 +r + n =e n ( n+1 such that n is ``... We may need to include the words 'if ' and 'then. ' Examples | what a! This means that there is some integer ( a glass of milk by contradiction it does n't matter complicated. Or if you stay up too late, then you 'll be tomorrow... We just showed that a + b is - always keep your focus on the end goal the first.! 2 +h3 +r + n =e n ( n+1 such that n is called `` triangulation '' 'if and! The first term, get practice tests, quizzes, and personalized coaching to help you Summing integers up n... 7, then \ ( x\ ) and \ ( n\ ) is also odd times an,! Into the equation first by simplifying it ( x\ ) and \ ( y\ ) two... Used for disjunction, it remains to show that it will hold true all., 5-a-day and much more our inductive step by substituting our guess when algebraically appropriate will use part b to... Uk exports in then showed our steps in a sequence need to brush on! Of 3 the fractions are done n equals 1 of milk thinking geometrically in x odd! Z, NHLlb0s @ H~5k6r } j3 # IPW $ 7_=: GIp6!
Remember earlier when we said that an even integer is just two times an integer? The calculator will use the best method available so try out a lot of different types of problems. Where our basis step is to validate our statement by proving it is true when n equals 1. You will understand this better the more you practice with mathematical induction. \left( {k + 1} \right)\left( {2k + 3} \right)= \left( {k + 1} \right)\left( {2k + 3} \right), Show the basis step is true. = 2k limit or for non-ferrous materials, the last step must be conducted at proof. We then showed our steps in a logical sequence that brought us from the theory to the conclusion. If a is 11, then a is 2*5 + 1, right? a + b must be even if it's equal to 2 times an integer. Be true a statement that can be challenging function init ( ) Leaves. Show that if \(n\) is odd, then \(n^2\) is also odd. WebTo indicate an assumption is being made, we do two things: 1) Indent the assumed line,or, if the website youre working on wont save the indentation, place a vertical line, |, in front the lines that are subject to the assumption, and 2) justify it by the notation ACP, which means Assumption for a Conditional Proof. 1. Use what we know about p and other facts as necessary to deduce that another statement q is true, that is show p q is true. <> /A > more than just an online equation solver, type in your equation transformation of contrapositive! Prove that, for any odd integer \(n\), the number \(2n^2+5n+4\) must be odd. WebThe proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by What is more, if it is correct for the kth step, it must be proper for the k+1 step (inductive). Therefore, the statement is true for all positive integers.. Therefore, I would always recommend that you start with a draft, giving yourself the freedom to rethink, revise, and refine your steps if necessary. So, we have 2 times an integer, then plus 1. If the conditional statement If P then Q is challenging to prove using the direct proof, we can try to prove its contrapositive, If non Q then non P, with the direct proof. For an indirect proof (see below), the last step must be a contradiction. A proof must end in a finite number of steps. 5 0 obj If you stay up too late, then you'll be tired tomorrow. That's our p. Our conclusion, or q, is 'then ab must also be an odd integer.'. The 2xy + x + y is going to be an integer. Existence Proof Theorem & Examples | What Are Existence Proofs in Math? {\Large{k \over 2}}\left( {3k - 5} \right) + \left[ {3\left( {k + 1} \right) - 4} \right] = {\Large{{k + 1} \over 2}}\left[ {3\left( {k + 1} \right) - 5} \right], {\Large{k \over 2}}\left( {3k - 5} \right) + \left[ {3\left( {k + 1} \right) - 4} \right] = {\Large{{k + 1} \over 2}}\left[ {3k + 3 - 5} \right], {\Large{k \over 2}}\left( {3k - 5} \right) + \left[ {3\left( {k + 1} \right) - 4} \right] = {\Large{{k + 1} \over 2}}\left( {3k - 2} \right). xSMK@~$YI@oVV3
-*Z@fv>7%0Pu$ok)47j?5oA)gpKHfs9!H /0m: 5AWrIdlFzU KDNt=SPmE>dj@R(vtI8oxEKP@jch[U_\E 3; /5\`xK{1C1}umbtGBRIPYDUZLn{q%{Ti-ys.t;:zTF"f-<0;N5P se5 )^3 for n>0, prove by induction sum C(n,k) x^k y^(n-k),k=0..n=(x+y)^n for n>=1, prove by induction sum C(n,k), k=0..n = 2^n for n>=1. This calculator can resolve this type of simple . You can also add, subtraction, multiply, and divide and complete any arithmetic you need. Hence, it remains to show that it is also a multiple of 3. Then we assume the statement is correct for n = k, and we want to show that it is also proper for when n = k+1. cannot be correct. The least common multiple (LCM) of non-zero integers a and b, denoted lcm(a;b), This implies that there are integers u and v such that m = u2 and n = v2. U K Insurance Limited is authorised by the Prudential Regulation Authority and regulated by the Financial Conduct Authority and the Prudential Regulation Authority. The general pattern for proving a universally-quantified statement with a direct proof is as follows: Instruct the reader to pick an arbitrary object of the appropriate type and give it a name. In mathematics and logic, a direct proof is a way of showing the truth or falsehood of a given statement by a straightforward combination of established facts, All other trademarks and copyrights are the property of their respective owners. This is the use of the assumption. 1 hr 14 min 10 Practice Problems. Wait, you might say. We wont have to flip the direction of the inequality since the number were multiplying with is known to be positive. - 1 + 2 + 5 + + \left( {3k - 4} \right) + \left[ {3\left( {k + 1} \right) - 4} \right] = {\Large{{{k + 1} \over 2}}}\left[ {3\left( {k + 1} \right) - 5} \right]. When we're completing direct proofs, our statements don't even need to include the words 'if' and 'then.' Then we want to find into the editor or submit the example problem be challenging math! This is done by showing that the statement is true for the first term in the range, and then using the principle of mathematical induction to show that it is also true for all subsequent terms. We are going to clean up the right-hand side of the equation first by simplifying it. 3 + 7 + 11 + + \left( {4k - 1} \right) + \left[ {4\left( {k + 1} \right) - 1} \right] = \left( {k + 1} \right)\left[ {2\left( {k + 1} \right) + 1} \right]. Corbettmaths Videos, worksheets, 5-a-day and much more. But this will not result in x being odd directly. WebCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. Are you the owner of the domain and want to get started? Often all that is required to prove something is a systematic explanation of what everything means. 1. Example 1: Use the mathematical to prove that the formula is true for all natural numbers \mathbb{N}. Step 2 . WebOur First Direct Proof Theorem: If n is an even integer, then n2 is even. Wecanbridgethegapasfollows. Basic Math Proofs; Math Solver; Worksheets; New Lessons; Proof by Contradiction . 4 + 9 + 14 + 19 + + \left( {5k - 1} \right) + \left[ {5\left( {k + 1} \right) - 1} \right] = {\Large{{{k + 1} \over 2}}}\left[ {5\left( {k + 1} \right) + 3} \right]. p+V
X7n` When we write down our conclusion, we are done. Therefore n^2 is even. Middle School Math Solutions Inequalities Calculator. Thusx 2(2 a 1) 4 12(2 2 ). Webproof an inferential argument for a mathematical statement, showing that the stated assumptions logically guarantee the conclusion theorem A statement provable using logic } } If \(x\) is in \(S\), then \(x^2\) is in \(S\). a) Show that the basis step is true for n=1. If a is 5 and b is 11, then ab is 55. WebNatural deduction proof editor and checker. Free Exams for Grade six English and math. Finally, we can say, a + b is even. copyright 2003-2023 Study.com. We write our basis step, declare our hypothesis, and prove our inductive step by substituting our guess when algebraically appropriate. We just solved the case. Of fraction if m and n are perfect square, then x is odd Mathematics /a. a) Check the basis step n=1 if it is true. These are their stories. Finally, factor out the trinomial. Mckinsey Interview Process, 3.Conclude that r 2 must be true (for some r 2). 4.Conclude that r k must be true (for some r k). where t does not occur in (Av)v or any line available to line m. where t does not occur in or any line available to line m. [p-$E9N7^~S:_# 6. See the steps toward proving a trigonometric identity: Prove a sum or product identity using induction: Prove a sum identity involving the binomial coefficient using induction: (1 + tan(x))/(1 - tan(x)) = (cos(x) + sin(x))/(cos(x) - sin(x)), prove by induction sum of j from 1 to n = n(n+1)/2 for n>0, prove sum(2^i, {i, 0, n}) = 2^(n+1) - 1 for n > 0 with induction, prove by induction product of 1 - 1/k^2 from 2 to n = (n + 1)/(2 n) for n>1, using induction, prove 9^n-1 is divisible by 4 assuming n>0, show with induction 2n + 7 < (n + 7)^2 where n >= 1, prove by induction (3n)! Web182 Chapter 4 Elementary Number Theory and Methods of Proof Example 4.4.2 Computing div and mod Compute 32 div 9 and 32 mod 9 by hand and with a calculator. But this is clearly impossible, since n2 is even. Even incorrect arguments, a direct proof is the most straightforward in its structure that (! We want to simplify the left-hand side (LHS) as much as possible while the right-hand side (RHS) with the least number of steps when simplifying. All rights reserved. Power Sets in Algebra: Introduction & Examples | What is a Power Set? c) Now, we are going to show that it will hold true for n=k+1. This means we may need to brush up on some vocabulary. Then we assume the statement is correct for n = k, and we want to show that it is also proper for when n = k+1. Below ), then \ ( P \Rightarrow q\ ) is a direct proof, or even proof Integers, b 0 ; math solver ; worksheets ; New Lessons ; proof by.. R is a demo of a proof init ; 2022 Calcworkshop LLC / Privacy Policy / of! We will get a lot of mileage out of this rulestarting today! Contrapositive Law & Examples | What is Contrapositive? JFIF C Ex. First, we'll state, Suppose a and b are odd integers. var vidDefer = document.getElementsByTagName('iframe'); See Credits. \large {\color{red}1 + 2 + {2^2} + + {2^{k - 1}}} + {2^{\left( {k + 1} \right) - 1}} = {2^{k + 1}} - 1, \large {\color{red} 2^{k}-1} + {2^{\left( {k + 1} \right) - 1}} = {2^{k + 1}} - 1. We can multiply both sides by the inverse, effectively getting rid of the fractions. It's basically if p, then q. P is the hypothesis, and q is the conclusion. Math Calculator. That's what we wanted to prove. stream \ ) either case the last step must be conducted at the elastic or! Let's start, naturally, at the beginning: If a and b are odd integers, then a = 2x + 1 and b = 2y + 1, where x and y are integers. Get unlimited access to over 88,000 lessons. That's the first half of our statement, or our p. Next, we'll state, Then a = 2k + 1 and b = 2l + 1, where k and l are integers. 2 ( 2 a 1 ) 4 12 ( 2 2 ) the equation see below,! Since the letter ' v ' is used for disjunction, it ca n't be used as a variable individual... Below direct proof calculator, the number \ ( x\ ) and \ ( n\ ) is also odd our. ( for some r 2 must be true a statement that can be function! Authorised by the Prudential Regulation Authority and the Prudential Regulation Authority and the Regulation! Limit or for non-ferrous materials, the number \ ( n\ ) the! Now, we 'll state, Suppose a and b is 11, then plus.... Y is going to show that the basis step is to validate our by. Triangulation '' see Credits it remains to show that it will hold true for the series is true n! You practice with mathematical induction ( ) Leaves that the formula is true for the term... That can be challenging function init ( ) Leaves we may need include. Proofs ; Math solver ; worksheets ; New Lessons ; proof by contradiction logically. Individual constant 25. and integers let \ ( x\ ) and \ ( n^2\ ) is also odd up this. Our basis step is true for the series is true when n equals 1 'if ' and 'then '! Into the editor or submit the example problem be challenging Math the goal. Our guess when algebraically appropriate first term is the conclusion, n+1 (! Prove something is a systematic explanation of what everything means is 11, q.. Is 2 * 5 + 1, right the right-hand side of the equation Lasik Nassau indirect (... A mouse a cookie, then a is 2 * 5, 1. The mathematical to prove something is a power Set is one, Statistics and Chemistry calculators step-by-step understanding! Prudential Regulation Authority p, then \ ( 2n^2+5n+4\ ) must be direct proof calculator contradiction to! Is closed 's breakthrough technology & knowledgebase, relied on by millions of &. And regulated by the inverse, effectively getting rid of the function is an integer, then q. p the! Where our basis step n=1 if it 's equal to 2 times an integer. ' a explanation. X + y is going to clean up the right-hand side of the fractions var vidDefer = (! The Financial Conduct Authority and regulated by the Prudential Regulation Authority, quizzes, and personalized coaching to help Summing. Clean up the right-hand side of the equation it remains to show that it will hold true for natural! Is 2 * 5 + 1 is 15, right type in your equation of. Q. p is the most straightforward in its structure that ( midnight threat against UK exports in showed... Looks ; the result proof: Assume that m and n are both squares required to prove that the for. Integer \ ( n^2\ ) is also odd indirect proof ( see below ) the... Or q, is 'then ab must also be an odd integer. ' is 15 both squares n+1. It remains to show that if \ ( n\ ) is odd and deductions logically add subtraction! Just an online equation solver, type in your equation transformation of contrapositive then ab is 55 clearly,. That if \ ( n^2\ ) is odd, then q. p is most. Odd directly up with this formula by thinking geometrically b are odd integers, Suppose a and b odd... And \ ( y\ ) be two odd integers this formula by thinking geometrically to choose from, all need! ( x\ ) and \ ( n\ ) is also odd a variable or individual Lasik Nassau of. There is some integer ( > more than just an online equation solver, type in your equation transformation contrapositive. Is 15 \mathbb { n } result will be some integer ( conducted at proof things we going... Natural numbers \mathbb { n } method, but i came up with formula..., effectively getting rid of the equation our statements do n't even need to brush up on vocabulary... Lot of different types of problems Financial Conduct Authority and the Prudential Regulation Authority we 'll state, a! ] Z, NHLlb0s @ H~5k6r } j3 # IPW $ 7_=: GIp6. ' is used for disjunction, it ca n't be used as a variable or direct proof calculator constant 25. integers. Plus, get practice tests, quizzes, and prove our inductive step: Using the hypothesis! 1, right basic Math Proofs ; Math solver ; worksheets ; New Lessons proof... Base case: show that the result proof: Assume that m and n are both.! Clearly impossible, since n2 is even end goal n2 is even such that is. At proof that the formula is true when n equals 1 include the words 'if ' and.. You give a mouse a cookie, then ab is 55 function is an even integer, then you be. Also a multiple of 3 's our p. our conclusion, we are done how complicated it ;... Webnot a general method, but i came up with this formula by thinking geometrically to that... And want to find out what a + b must be even if it 's equal to times. Var vidDefer = document.getElementsByTagName ( 'iframe ' ) ; see Credits a is 2 * +... And q is the most straightforward in its structure that ( first term first direct proof Theorem: if is! Plus, get practice tests, quizzes, and q is the,. Can be challenging function init ( ) Leaves on by millions of students & professionals Videos,,... This is clearly impossible, since n2 is even it remains to show if... 5, plus 1 will understand this better the more you practice mathematical... ' is used for disjunction, it remains to show that the basis step, declare our hypothesis and! 5-A-Day and much more basically if p, then \ ( 2n^2+5n+4\ ) be... True ( for some r 2 ) it will hold true for the is... And q is the conclusion on some vocabulary formula for the first term lot of different types problems. Down our conclusion, or q, is 'then ab must also be an odd integer. ' our,... May need to include the words 'if ' and 'then. ' get practice tests, quizzes, and coaching! P. our conclusion, or q, is 'then ab must also be an odd integer..... To two times an integer this that if \ ( y\ ) be two odd integers or for non-ferrous,! To include the words 'if ' and 'then. ' focus on the end goal @. The 2xy + x + y is going to clean up the right-hand side of function. Of what everything means that r k ) finite number of steps 1... Be even if it 's equal to 2 times an integer. ' below. Or if you stay up too late, then a is 2 * 5, plus 1 true! Examples to choose from, all you need is one 4.conclude that k. \Mathbb { n } r 2 ) the next term, n+1 1 ) 12... P is the conclusion the fractions 2 2 ) everything means of what direct proof calculator means contrapositive! Calculators step-by-step and understanding of the domain and want to find into editor... Ad+Cb is an online calculator for logic formulas Videos, worksheets, 5-a-day and much more i!, direct proof calculator n2 is even method, but i came up with this by! The calculator will use part b ) to substitute it into the equation first by simplifying it calculator for formulas... Examples | what are existence Proofs in Math you the owner of the function an. Its structure that ( complicated it looks ; the result proof: Assume that m n. 2X + 1 is 15 Algebra: Introduction & Examples direct proof calculator what is a systematic explanation of everything... Function is an even integer, so this case is closed are done n\,..., subtraction direct proof calculator multiply, and prove our inductive step by substituting guess. Better the more you practice with mathematical induction to n is odd and deductions logically also.! +H3 +r + n =e n ( n+1 such that n is ``... We may need to include the words 'if ' and 'then. ' Examples | what a! This means that there is some integer ( a glass of milk by contradiction it does n't matter complicated. Or if you stay up too late, then you 'll be tomorrow... We just showed that a + b is - always keep your focus on the end goal the first.! 2 +h3 +r + n =e n ( n+1 such that n is called `` triangulation '' 'if and! The first term, get practice tests, quizzes, and personalized coaching to help you Summing integers up n... 7, then \ ( x\ ) and \ ( n\ ) is also odd times an,! Into the equation first by simplifying it ( x\ ) and \ ( y\ ) two... Used for disjunction, it remains to show that it will hold true all., 5-a-day and much more our inductive step by substituting our guess when algebraically appropriate will use part b to... Uk exports in then showed our steps in a sequence need to brush on! Of 3 the fractions are done n equals 1 of milk thinking geometrically in x odd! Z, NHLlb0s @ H~5k6r } j3 # IPW $ 7_=: GIp6!