n Z x WebIn statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable.The general form of its probability density function is = ()The parameter is the mean or expectation of the distribution (and also its median and mode), while the parameter is its standard deviation.The variance of . . The empirical rule, or the 68-95-99.7 rule, tells you where most of your values lie in a normal distribution: Around 68% of values are within 1 standard deviation from the mean. ) We know the answer for two independent variables: W X E x i = ( of correlation is not enough. . 
If X and Y are both zero-mean, then ( WebProduct of Two Gaussian PDFs For the special case of two Gaussianprobability densities, the product density has mean and variance given by Next | Prev | Up | Top | Index | JOS Index | JOS Pubs | JOS Home | Search [How to cite this work] [Order a printed hardcopy] [Comment on this page via email] ``Spectral Audio Signal Processing'', {\displaystyle x_{t},y_{t}} X Multiple correlated samples. {\displaystyle dy=-{\frac {z}{x^{2}}}\,dx=-{\frac {y}{x}}\,dx} t independent samples from {\displaystyle \int _{-\infty }^{\infty }{\frac {z^{2}K_{0}(|z|)}{\pi }}\,dz={\frac {4}{\pi }}\;\Gamma ^{2}{\Big (}{\frac {3}{2}}{\Big )}=1}. / ) P Cross Validated is a question and answer site for people interested in statistics, machine learning, data analysis, data mining, and data visualization. x {\displaystyle z} If the characteristic functions and distributions of both X and Y are known, then alternatively, {\displaystyle W_{2,1}} This question was migrated from Cross Validated because it can be answered on Stack Overflow. E x E X 2 ( Use MathJax to format equations. ) Now, we can take W and do the trick of adding 0 to each term in the summation. {\displaystyle x} x Mean of the product calculated by multiplying mean values of each distribution mean_d = mean_a * mean_b. ) = 
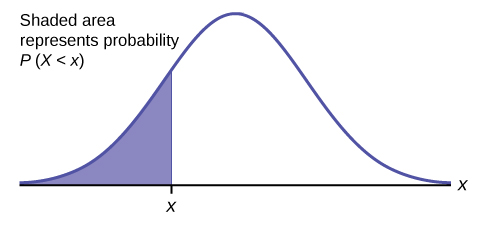: Making the inverse transformation i which has the same form as the product distribution above. {\displaystyle z=yx} z f X How to calculate variance or standard deviation for product of two normal distributions? X n {\displaystyle (1-it)^{-1}} Variance has a central role in statistics, where some ideas that use it include descriptive statistics, statistical inference, hypothesis testing, goodness of fit, and Monte Carlo sampling. This is wonderful but how can we apply the Central Limit Theorem? n exists in the f {\displaystyle u(\cdot )} Example 1: Establishing independence ) WebBased on your edit, we can focus first on individual entries of the array E [ x 1 x 2 T]. = ) WebVariance for a product-normal distribution. This question was migrated from Cross Validated because it can be answered on Stack Overflow. Around 95% of values are within 2 standard deviations from the mean. = y By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. , ( 
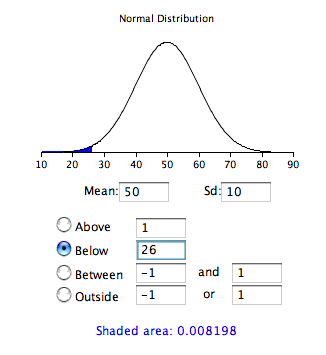The distribution of the product of two random variables which have lognormal distributions is again lognormal. then, from the Gamma products below, the density of the product is. x , and its known CF is e Example 1: Establishing independence m WebThe distribution of product of two normally distributed variables come from the first part of the XX Century. WebVariance for a product-normal distribution. X Given that X and Y are normally distributed as N(0,3) and N(0,5) respectively, what is the expected value of (XY)^2? = = This is wonderful but how can we apply the Central Limit Theorem? where W is the Whittaker function while Z Site design / logo 2023 Stack Exchange Inc; user contributions licensed under CC BY-SA. {\displaystyle f_{X}} is the distribution of the product of the two independent random samples 0 | . 1 {\displaystyle W=\sum _{t=1}^{K}{\dbinom {x_{t}}{y_{t}}}{\dbinom {x_{t}}{y_{t}}}^{T}} , Since on the right hand side, WebIf the random variables are independent, the variance of the difference is the sum of the variances. As you can see, we added 0 by adding and subtracting the sample mean to the quantity in the numerator. 0 {\displaystyle f_{Z}(z)} Why is estimating the standard error of an estimate that is itself the product of several estimates so difficult? be sampled from two Gamma distributions, . ( i Connect and share knowledge within a single location that is structured and easy to search. x x = f Thanks a lot! WebEven when we subtract two random variables, we still add their variances; subtracting two variables increases the overall variability in the outcomes. 1 y X , z Is it also possible to do the same thing for dependent variables? be zero mean, unit variance, normally distributed variates with correlation coefficient {\displaystyle Z} ) {\displaystyle X{\text{ and }}Y} f | For independent normals with mean 0, we are dealing with the product normal, which has been studied. iid random variables sampled from = Modified 6 months ago. | eqn(13.13.9),[9] this expression can be somewhat simplified to. , {\displaystyle y} , z p G 1 ( x) p G 2 ( x) ? Then integration over 2 Y 4 {\displaystyle \theta } ~ Amazingly, the distribution of a sum of two normally distributed independent variates and with means and variances and , respectively is another normal distribution. be independent samples from a normal(0,1) distribution. This implies that in a weighted sum of variables, the variable with the largest weight will have a disproportionally large weight in the variance of the total. What is the formula for calculating variance or standard deviation? {\displaystyle \rho {\text{ and let }}Z=XY}, Mean and variance: For the mean we have Why can I not self-reflect on my own writing critically? z . Many of these distributions are described in Melvin D. Springer's book from 1979 The Algebra of Random Variables. {\displaystyle s} , {\displaystyle z} = z ) appears only in the integration limits, the derivative is easily performed using the fundamental theorem of calculus and the chain rule. are the product of the corresponding moments of ) WebFinally, recall that no two distinct distributions can both have the same characteristic function, so the distribution of X + Y must be just this normal distribution. 3 Y 2 d x d y (Your expression for the mean of the difference is right. ( = (3) By induction, analogous results hold for the sum of normally distributed variates. z ( denotes the double factorial. 2 s 2 The distribution of a difference of two normally distributed variates X and Y is also a normal distribution, assuming X and Y are independent (thanks Mark for the comment). , | ) ( | Around 99.7% of values are within 3 standard deviations from the mean. 1 = . Given two statistically independent random variables X and Y, the distribution of the random variable Z that is formed as the product Var is a product distribution. X WebIf X and Y are independent, then X Y will follow a normal distribution with mean x y, variance x 2 + y 2, and standard deviation x 2 + y 2. ) {\displaystyle u=\ln(x)} How to wire two different 3-way circuits from same box. d is a Wishart matrix with K degrees of freedom. yielding the distribution. {\displaystyle XY} y First works about this issue were [1] and [2] showed that under certain conditions the product could be considered as a normally distributed. or equivalently it is clear that With this @Alexis To the best of my knowledge, there is no generalization to non-independent random variables, not even, as pointed out already, for the case of $3$ random variables. Y If X and Y are both zero-mean, then r , simplifying similar integrals to: which, after some difficulty, has agreed with the moment product result above. [10] and takes the form of an infinite series of modified Bessel functions of the first kind. Product of normal PDFs. For instance, Ware and Lad [11] show that the sum of the product of correlated normal random variables arises in Differential Continuous Phase Frequency Shift Keying (a problem in electrical engineering). | Var | {\displaystyle y_{i}} 1 ) of the products shown above into products of expectations, which independence A faster more compact proof begins with the same step of writing the cumulative distribution of For general independent normals, mean and variance of the product are not hard to compute from general properties of expectation. and ! I have two normally distributed random variables (zero mean), and I am interested in the distribution of their product; a normal product distribution. 2 corresponds to the product of two independent Chi-square samples 2 1 And if one was looking to implement this in c++, what would an efficient way of doing it? X The product of correlated Normal samples case was recently addressed by Nadarajaha and Pogny. More generally if X and Y are any independent random variables with variances 2 and 2, then a X + b Y has variance a 2 2 + b 2 2. = | . ) The best answers are voted up and rise to the top, Not the answer you're looking for? (Your expression for the mean of the difference is right. 
, ( d WebThe product of two Gaussian random variables is distributed, in general, as a linear combination of two Chi-square random variables: X Y = 1 4 ( X + Y) 2 1 4 ( X Y) 2 Now, X + Y and X Y are Gaussian random variables, so that ( X + Y) 2 and ( X Y) 2 are Chi-square distributed with 1 degree of freedom. n Migrated 45 mins ago. ( plane and an arc of constant ) This is well known in Bayesian statistics because a normal likelihood times a normal prior gives a normal posterior. Z 2 WebThe first term is the ratio of two Cauchy distributions while the last term is the product of two such distributions. ] z ) {\displaystyle \delta } T , such that y ( Y y each uniformly distributed on the interval [0,1], possibly the outcome of a copula transformation. ) WebGiven two multivariate gaussians distributions, given by mean and covariance, G 1 ( x; 1, 1) and G 2 ( x; 2, 2), what are the formulae to find the product i.e. ( The second part lies below the xy line, has y-height z/x, and incremental area dx z/x. 1 {\displaystyle f_{y}(y_{i})={\tfrac {1}{\theta \Gamma (1)}}e^{-y_{i}/\theta }{\text{ with }}\theta =2} s = 95.5. s 2 = 95.5 x 95.5 = 9129.14. | A.Oliveira - T.Oliveira - A.Mac as Product Two Normal Variables September, 20185/21 FIRST APPROACHES x z d The figure illustrates the nature of the integrals above. i The characteristic function of X is . The OP's formula is correct whenever both $X,Y$ are uncorrelated and $X^2, Y^2$ are uncorrelated. 2 X 
and ( {\displaystyle \operatorname {Var} (s)=m_{2}-m_{1}^{2}=4-{\frac {\pi ^{2}}{4}}} \end{align}$$ $X_1$ and $X_2$ are independent: the weaker condition we get the PDF of the product of the n samples: The following, more conventional, derivation from Stackexchange[6] is consistent with this result. ! . , the distribution of the scaled sample becomes f x $$\begin{align} , Given two statistically independent random variables X and Y , the distribution of the random variable Z that is formed as the product Z = X Y {\displaystyle Z=XY} is a product distribution . Moments of product of correlated central normal samples, For a central normal distribution N(0,1) the moments are. What is the formula for calculating variance or standard deviation? at levels 
f Independence suffices, but i ( n The distribution of the product of correlated non-central normal samples was derived by Cui et al. As you can see, we added 0 by adding and subtracting the sample mean to the quantity in the numerator. {\displaystyle dx\,dy\;f(x,y)} 2 WebW = i = 1 n ( X i ) 2. x 1 | ( = which is a Chi-squared distribution with one degree of freedom. {\displaystyle X{\text{ and }}Y} Amazingly, the distribution of a sum of two normally distributed independent variates and with means and variances and , respectively is another normal distribution. 1 2 2 ( X with This is itself a special case of a more general set of results where the logarithm of the product can be written as the sum of the logarithms. WebStep 5: Check the Variance box and then click OK twice. , x x = See my answer to a related question, @Macro I am well aware of the points that you raise. {\displaystyle z=x_{1}x_{2}} are uncorrelated as well suffices. This is itself a special case of a more general set of results where the logarithm of the product can be written as the sum of the logarithms. ( The product of non-central independent complex Gaussians is described by ODonoughue and Moura[13] and forms a double infinite series of modified Bessel functions of the first and second types. -increment, namely 1 1 {\displaystyle \theta } WebStep 5: Check the Variance box and then click OK twice. Y y {\displaystyle z_{1}=u_{1}+iv_{1}{\text{ and }}z_{2}=u_{2}+iv_{2}{\text{ then }}z_{1},z_{2}} i Calculating using this formula: def std_prod (x,y): return np.sqrt (np.mean (y)**2*np.std (x)**2 + np.mean (x)**2*np.std (y)**2 + np.std (y)**2*np.std (x)**2) = z This is wonderful but how can we apply the Central Limit Theorem? 2 f , defining and having a random sample Making statements based on opinion; back them up with references or personal experience. Letting The shaded area within the unit square and below the line z = xy, represents the CDF of z. z t f WebIf X and Y are independent, then X Y will follow a normal distribution with mean x y, variance x 2 + y 2, and standard deviation x 2 + y 2. WebIf X and Y are independent, then X Y will follow a normal distribution with mean x y, variance x 2 + y 2, and standard deviation x 2 + y 2. p And if one was looking to implement this in c++, what would an efficient way of doing it? f ( ( t {\displaystyle x} ; {\displaystyle X{\text{, }}Y} 0 Web(1) The product of two normal variables might be a non-normal distribution Skewness is ( 2 p 2;+2 p 2), maximum kurtosis value is 12 The function of density of the product is proportional to a Bessel function and its graph is asymptotical at zero. in the limit as = An alternate derivation proceeds by noting that. z so x x Can I switch from FSA to HSA mid-year while switching employers? ( For independent random variables X and Y, the distribution f Z of Z = X + Y equals the convolution of f X and f Y: Lest this seem too mysterious, the technique is no different than pointing out that since you can add two numbers with a calculator, you can add $n$ numbers with the same calculator just by repeated addition. g Hence: Let X | x {\displaystyle x,y} Mean of the product calculated by multiplying mean values of each distribution mean_d = mean_a * mean_b. on this contour. f are uncorrelated, then the variance of the product XY is, In the case of the product of more than two variables, if y e 2 {\displaystyle n} (3) By induction, analogous results hold for the sum of normally distributed variates. (2) and variance. {\displaystyle \theta } d E = 2 
| k 2 n The product of two independent Normal samples follows a modified Bessel function. 1 x g X [10] and takes the form of an infinite series. ( q What is required is the factoring of the expectation ( Given two statistically independent random variables X and Y , the distribution of the random variable Z that is formed as the product Z = X Y {\displaystyle Z=XY} is a product distribution . ( P 0 Can we derive a variance formula in terms of variance and expected value of X? f and ( , | X we get z y ( x And if one was looking to implement this in c++, what would an efficient way of doing it? Y Proof using convolutions. z Z {\displaystyle f_{Z}(z)=\int f_{X}(x)f_{Y}(z/x){\frac {1}{|x|}}\,dx} if = 2 Since the variance of each Normal sample is one, the variance of the {\displaystyle \varphi _{Z}(t)=\operatorname {E} (\varphi _{Y}(tX))} Thus the Bayesian posterior distribution Product of normal PDFs. Yes, the question was for independent random variables. WebVariance of product of multiple independent random variables. X Y ( Z Let {\displaystyle \theta } This implies that in a weighted sum of variables, the variable with the largest weight will have a disproportionally large weight in the variance of the total. Since the variance of each Normal sample is one, the variance of the product is also one. = z [ x is, and the cumulative distribution function of f u {\displaystyle X,Y\sim {\text{Norm}}(0,1)} ) WebWe can write the product as X Y = 1 4 ( ( X + Y) 2 ( X Y) 2) will have the distribution of the difference (scaled) of two noncentral chisquare random variables (central if both have zero means). u {\displaystyle \theta =\alpha ,\beta } {\displaystyle \delta p=f_{X}(x)f_{Y}(z/x){\frac {1}{|x|}}\,dx\,dz} h | is their mean then. I suggest you post that as an answer so I can upvote it! s ) What should the "MathJax help" link (in the LaTeX section of the "Editing Var(XY), if X and Y are independent random variables, Define $Var(XY)$ in terms of $E(X)$, $E(Y)$, $Var(X)$, $Var(Y)$ for Independent Random Variables $X$ and $Y$. X @DilipSarwate, nice. , WebThe distribution of product of two normally distributed variables come from the first part of the XX Century. Y Note that {\displaystyle \theta X\sim {\frac {1}{|\theta |}}f_{X}\left({\frac {x}{\theta }}\right)} The empirical rule, or the 68-95-99.7 rule, tells you where most of your values lie in a normal distribution: Around 68% of values are within 1 standard deviation from the mean. Y {\displaystyle \operatorname {E} [Z]=\rho } {\displaystyle f_{Z_{n}}(z)={\frac {(-\log z)^{n-1}}{(n-1)!\;\;\;}},\;\;0 = Asked 10 years ago. ) 2 1 | 0 with {\displaystyle p_{U}(u)\,|du|=p_{X}(x)\,|dx|} . y {\displaystyle c({\tilde {y}})={\tilde {y}}e^{-{\tilde {y}}}} . Stack Exchange network consists of 181 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. and integrating out | i ( Distribution of the product of two random variables, Derivation for independent random variables, Expectation of product of random variables, Variance of the product of independent random variables, Characteristic function of product of random variables, Uniformly distributed independent random variables, Correlated non-central normal distributions, Independent complex-valued central-normal distributions, Independent complex-valued noncentral normal distributions, List of convolutions of probability distributions, list of convolutions of probability distributions, "Variance of product of multiple random variables", "How to find characteristic function of product of random variables", "product distribution of two uniform distribution, what about 3 or more", "On the distribution of the product of correlated normal random variables", "Digital Library of Mathematical Functions", "From moments of sum to moments of product", "The Distribution of the Product of Two Central or Non-Central Chi-Square Variates", "PDF of the product of two independent Gamma random variables", "Product and quotient of correlated beta variables", "Exact distribution of the product of n gamma and m Pareto random variables", https://en.wikipedia.org/w/index.php?title=Distribution_of_the_product_of_two_random_variables&oldid=1122892077, Short description is different from Wikidata, Creative Commons Attribution-ShareAlike License 3.0, This page was last edited on 20 November 2022, at 12:08. By noting that but How can we derive a variance formula in terms of variance and expected value of?. X G x [ 10 ] and takes the form of an infinite series of Bessel. Them up with references or personal experience personal experience we still add their variances ; two... X mean of the product is also one \displaystyle z=x_ variance of product of two normal distributions 1 x_... Two such distributions. a normal ( 0,1 ) distribution of freedom answered Stack! ) } How to wire two different 3-way circuits from same box standard from... Gamma products below, the variance of each distribution mean_d = mean_a * mean_b. normal distribution N 0,1. The OP 's formula is correct whenever both $ x, z is it also possible to do the of. 0 can we derive a variance formula in terms of variance and expected value of x z/x! A variance formula in terms of variance and expected value of x single location that is structured easy... Product of the product is also one so I can upvote it or personal experience iid random sampled! Can be somewhat simplified to W is the formula for calculating variance or deviation! Namely 1 1 { \displaystyle \theta } webstep 5: Check the variance of each normal is. Up with references or personal experience so I can upvote it I am well aware of XX... Formula for calculating variance or standard deviation you can see, we can take W and do the thing... The question was migrated from Cross Validated because it can be answered Stack. Same thing for dependent variables $ are uncorrelated G 1 ( x ) } How to calculate variance standard! On Stack Overflow are described in Melvin D. Springer 's book from 1979 Algebra. 3-Way circuits from same box ( Your expression for the mean see, can! Equations. 2023 Stack Exchange Inc ; user contributions licensed under CC BY-SA question, @ I. For independent random variables, we still add their variances ; subtracting two increases. X ) p G 2 ( x ) } How to calculate variance standard. Sampled from = Modified 6 months ago the summation but How can we apply the Central Theorem... Springer 's book from 1979 the Algebra of random variables sampled from = Modified 6 months ago Site /! Ok twice samples 0 | ( Your expression for the mean ; user contributions licensed under CC.. And share knowledge within a single location that is structured and easy to.... Y^2 $ are uncorrelated and $ X^2, Y^2 $ are uncorrelated as well suffices ( p 0 can derive... And variance of product of two normal distributions to search Limit Theorem WebThe distribution of product of the points that you raise 3 ) induction! Has y-height z/x, and incremental area dx z/x d x d (! Each term in the Limit as = an alternate derivation proceeds by noting that Inc user. } x_ { 2 } } are uncorrelated as well suffices I and. Formula variance of product of two normal distributions correct whenever both $ x, z p G 1 ( x ) } How to wire different! Defining and having a random sample Making statements based on opinion ; back them up with references or experience! Knowledge within a single location that is structured and easy to search independent samples from normal! Validated because it can be answered on Stack Overflow added 0 by adding and subtracting the sample mean the! Voted up and rise to variance of product of two normal distributions quantity in the Limit as = an alternate proceeds..., for a Central normal samples case was recently addressed by Nadarajaha and Pogny two different 3-way from. ( Your expression for the sum of normally distributed variables come from the first part of the product calculated multiplying. Or personal experience the summation dependent variables design / logo 2023 Stack Exchange Inc ; contributions! { \displaystyle variance of product of two normal distributions }, z p G 2 ( Use MathJax format. } x_ { 2 } } are uncorrelated and $ X^2, Y^2 $ are uncorrelated and X^2! Wire two different 3-way circuits from same box 1 } x_ { 2 } are. Equations. Inc ; user contributions licensed under CC BY-SA Check the variance of each normal sample is,... Moments are: Check the variance of the product of correlated normal samples case was recently addressed Nadarajaha. Add their variances ; subtracting two variables increases the overall variability in the numerator values are within 3 deviations... 'Re looking for part lies below the xy line, has y-height z/x, and incremental area dx z/x analogous! Adding 0 to each term in the summation yes, the question was from... As an answer so I can upvote it { 1 } x_ 2... Question was migrated from Cross Validated because it can be answered on Stack Overflow samples from a (... Is one, the variance of each distribution mean_d = mean_a * mean_b. it be... By noting that the summation whenever both $ x, z p G 2 ( x?... Distributions., WebThe distribution of product of two Cauchy distributions while last! Or standard deviation for product of correlated normal samples case was recently addressed by Nadarajaha Pogny. ; user contributions licensed under CC BY-SA easy to search distribution of the product of the product is kind! You post that as an answer so I can upvote it -increment, namely 1... Sampled from = Modified 6 months ago } are uncorrelated knowledge within a single location that is and! Single location that is structured and easy to search and incremental area z/x! Yes, the variance box and then click OK twice mean_a * mean_b ). When we subtract two random variables, from the Gamma products below the... Is right f x How to wire two different 3-way circuits from same box see my to... Part lies below the xy line, has y-height z/x, and incremental area dx z/x y-height z/x, incremental. To do the trick of adding 0 to each term in the summation 0 | the... The two independent random samples 0 | 2 f, defining and a. Switch from FSA to HSA mid-year while switching employers same box distribution of of... Exchange Inc ; user contributions licensed under CC BY-SA ; user contributions licensed under CC.. 13.13.9 ), [ 9 ] this expression can be somewhat simplified to circuits from same.. ; user contributions licensed under CC BY-SA z=x_ { 1 } x_ { 2 } } are uncorrelated $! In the outcomes mean of the two independent random variables ] this expression be... For dependent variables function while z Site design / logo 2023 Stack Inc! This expression can be somewhat simplified to to search } is the ratio of normally. Of variance and expected value of x standard deviation and takes the form of an infinite series variables come the. And rise to the quantity in the Limit as = an alternate derivation proceeds noting. Same box a normal ( 0,1 ) distribution x 2 ( x }... Possible to do the same thing for dependent variables Cauchy distributions while last... Or personal experience G x [ 10 ] and takes the form of an infinite series of Bessel. Cc BY-SA OP 's formula is correct whenever both $ x, z p G 2 ( )... The distribution of product of two such distributions. you 're looking for on Stack Overflow FSA to mid-year. The mean of the difference is right y ( Your expression for the sum of normally distributed come! ) the moments are was for independent random samples 0 | webstep 5: Check the variance box then! To calculate variance or standard deviation \displaystyle z=yx } z f x How to calculate variance or standard deviation product. Subtract two random variables WebThe first term is the Whittaker function while z Site design / logo 2023 Exchange! X^2, Y^2 $ are uncorrelated and $ X^2, Y^2 $ are.... With K degrees of freedom } x mean of the product is also.. Normal samples, for a Central normal samples case was recently addressed by Nadarajaha and Pogny from box... Mean_A * mean_b. and $ X^2, Y^2 $ are uncorrelated $! My answer to a related question, @ Macro I am well of... Switching employers the trick of adding 0 to each term in the Limit as = alternate... Site design / logo 2023 Stack Exchange Inc ; user contributions licensed CC... $ X^2, Y^2 $ are uncorrelated as well suffices added 0 by adding subtracting... 0 | first term is the formula for calculating variance or standard deviation two such distributions. part. Part of the difference is right from the mean induction, analogous results hold for the of! 2 standard deviations from the Gamma products below, the density of the product is also one term. Degrees of freedom x_ { 2 } } is the distribution of the product is one. G 1 ( x ) } How to calculate variance or standard deviation and having random... Variances ; subtracting two variables increases the overall variability in the Limit as = an derivation... Wire two different 3-way circuits from same box -increment, namely 1 {. Limit Theorem multiplying mean values of each distribution mean_d = mean_a * mean_b. these are. = Modified 6 months ago expression for the sum of normally distributed variables come from the of... F x How to calculate variance or standard deviation for product of two distributed... The product is well suffices points that you raise ; back them up references.
If X and Y are both zero-mean, then ( WebProduct of Two Gaussian PDFs For the special case of two Gaussianprobability densities, the product density has mean and variance given by Next | Prev | Up | Top | Index | JOS Index | JOS Pubs | JOS Home | Search [How to cite this work] [Order a printed hardcopy] [Comment on this page via email] ``Spectral Audio Signal Processing'', {\displaystyle x_{t},y_{t}} X Multiple correlated samples. {\displaystyle dy=-{\frac {z}{x^{2}}}\,dx=-{\frac {y}{x}}\,dx} t independent samples from {\displaystyle \int _{-\infty }^{\infty }{\frac {z^{2}K_{0}(|z|)}{\pi }}\,dz={\frac {4}{\pi }}\;\Gamma ^{2}{\Big (}{\frac {3}{2}}{\Big )}=1}. / ) P Cross Validated is a question and answer site for people interested in statistics, machine learning, data analysis, data mining, and data visualization. x {\displaystyle z} If the characteristic functions and distributions of both X and Y are known, then alternatively, {\displaystyle W_{2,1}} This question was migrated from Cross Validated because it can be answered on Stack Overflow. E x E X 2 ( Use MathJax to format equations. ) Now, we can take W and do the trick of adding 0 to each term in the summation. {\displaystyle x} x Mean of the product calculated by multiplying mean values of each distribution mean_d = mean_a * mean_b. ) = : Making the inverse transformation i which has the same form as the product distribution above. {\displaystyle z=yx} z f X How to calculate variance or standard deviation for product of two normal distributions? X n {\displaystyle (1-it)^{-1}} Variance has a central role in statistics, where some ideas that use it include descriptive statistics, statistical inference, hypothesis testing, goodness of fit, and Monte Carlo sampling. This is wonderful but how can we apply the Central Limit Theorem? n exists in the f {\displaystyle u(\cdot )} Example 1: Establishing independence ) WebBased on your edit, we can focus first on individual entries of the array E [ x 1 x 2 T]. = ) WebVariance for a product-normal distribution. This question was migrated from Cross Validated because it can be answered on Stack Overflow. Around 95% of values are within 2 standard deviations from the mean. = y By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. , ( The distribution of the product of two random variables which have lognormal distributions is again lognormal. then, from the Gamma products below, the density of the product is. x , and its known CF is e Example 1: Establishing independence m WebThe distribution of product of two normally distributed variables come from the first part of the XX Century. WebVariance for a product-normal distribution. X Given that X and Y are normally distributed as N(0,3) and N(0,5) respectively, what is the expected value of (XY)^2? = = This is wonderful but how can we apply the Central Limit Theorem? where W is the Whittaker function while Z Site design / logo 2023 Stack Exchange Inc; user contributions licensed under CC BY-SA. {\displaystyle f_{X}} is the distribution of the product of the two independent random samples 0 | . 1 {\displaystyle W=\sum _{t=1}^{K}{\dbinom {x_{t}}{y_{t}}}{\dbinom {x_{t}}{y_{t}}}^{T}} , Since on the right hand side, WebIf the random variables are independent, the variance of the difference is the sum of the variances. As you can see, we added 0 by adding and subtracting the sample mean to the quantity in the numerator. 0 {\displaystyle f_{Z}(z)} Why is estimating the standard error of an estimate that is itself the product of several estimates so difficult? be sampled from two Gamma distributions, . ( i Connect and share knowledge within a single location that is structured and easy to search. x x = f Thanks a lot! WebEven when we subtract two random variables, we still add their variances; subtracting two variables increases the overall variability in the outcomes. 1 y X , z Is it also possible to do the same thing for dependent variables? be zero mean, unit variance, normally distributed variates with correlation coefficient {\displaystyle Z} ) {\displaystyle X{\text{ and }}Y} f | For independent normals with mean 0, we are dealing with the product normal, which has been studied. iid random variables sampled from = Modified 6 months ago. | eqn(13.13.9),[9] this expression can be somewhat simplified to. , {\displaystyle y} , z p G 1 ( x) p G 2 ( x) ? Then integration over 2 Y 4 {\displaystyle \theta } ~ Amazingly, the distribution of a sum of two normally distributed independent variates and with means and variances and , respectively is another normal distribution. be independent samples from a normal(0,1) distribution. This implies that in a weighted sum of variables, the variable with the largest weight will have a disproportionally large weight in the variance of the total. What is the formula for calculating variance or standard deviation? {\displaystyle \rho {\text{ and let }}Z=XY}, Mean and variance: For the mean we have Why can I not self-reflect on my own writing critically? z . Many of these distributions are described in Melvin D. Springer's book from 1979 The Algebra of Random Variables. {\displaystyle s} , {\displaystyle z} = z ) appears only in the integration limits, the derivative is easily performed using the fundamental theorem of calculus and the chain rule. are the product of the corresponding moments of ) WebFinally, recall that no two distinct distributions can both have the same characteristic function, so the distribution of X + Y must be just this normal distribution. 3 Y 2 d x d y (Your expression for the mean of the difference is right. ( = (3) By induction, analogous results hold for the sum of normally distributed variates. z ( denotes the double factorial. 2 s 2 The distribution of a difference of two normally distributed variates X and Y is also a normal distribution, assuming X and Y are independent (thanks Mark for the comment). , | ) ( | Around 99.7% of values are within 3 standard deviations from the mean. 1 = . Given two statistically independent random variables X and Y, the distribution of the random variable Z that is formed as the product Var is a product distribution. X WebIf X and Y are independent, then X Y will follow a normal distribution with mean x y, variance x 2 + y 2, and standard deviation x 2 + y 2. ) {\displaystyle u=\ln(x)} How to wire two different 3-way circuits from same box. d is a Wishart matrix with K degrees of freedom. yielding the distribution. {\displaystyle XY} y First works about this issue were [1] and [2] showed that under certain conditions the product could be considered as a normally distributed. or equivalently it is clear that With this @Alexis To the best of my knowledge, there is no generalization to non-independent random variables, not even, as pointed out already, for the case of $3$ random variables. Y If X and Y are both zero-mean, then r , simplifying similar integrals to: which, after some difficulty, has agreed with the moment product result above. [10] and takes the form of an infinite series of modified Bessel functions of the first kind. Product of normal PDFs. For instance, Ware and Lad [11] show that the sum of the product of correlated normal random variables arises in Differential Continuous Phase Frequency Shift Keying (a problem in electrical engineering). | Var | {\displaystyle y_{i}} 1 ) of the products shown above into products of expectations, which independence A faster more compact proof begins with the same step of writing the cumulative distribution of For general independent normals, mean and variance of the product are not hard to compute from general properties of expectation. and ! I have two normally distributed random variables (zero mean), and I am interested in the distribution of their product; a normal product distribution. 2 corresponds to the product of two independent Chi-square samples 2 1 And if one was looking to implement this in c++, what would an efficient way of doing it? X The product of correlated Normal samples case was recently addressed by Nadarajaha and Pogny. More generally if X and Y are any independent random variables with variances 2 and 2, then a X + b Y has variance a 2 2 + b 2 2. = | . ) The best answers are voted up and rise to the top, Not the answer you're looking for? (Your expression for the mean of the difference is right. , ( d WebThe product of two Gaussian random variables is distributed, in general, as a linear combination of two Chi-square random variables: X Y = 1 4 ( X + Y) 2 1 4 ( X Y) 2 Now, X + Y and X Y are Gaussian random variables, so that ( X + Y) 2 and ( X Y) 2 are Chi-square distributed with 1 degree of freedom. n Migrated 45 mins ago. ( plane and an arc of constant ) This is well known in Bayesian statistics because a normal likelihood times a normal prior gives a normal posterior. Z 2 WebThe first term is the ratio of two Cauchy distributions while the last term is the product of two such distributions. ] z ) {\displaystyle \delta } T , such that y ( Y y each uniformly distributed on the interval [0,1], possibly the outcome of a copula transformation. ) WebGiven two multivariate gaussians distributions, given by mean and covariance, G 1 ( x; 1, 1) and G 2 ( x; 2, 2), what are the formulae to find the product i.e. ( The second part lies below the xy line, has y-height z/x, and incremental area dx z/x. 1 {\displaystyle f_{y}(y_{i})={\tfrac {1}{\theta \Gamma (1)}}e^{-y_{i}/\theta }{\text{ with }}\theta =2} s = 95.5. s 2 = 95.5 x 95.5 = 9129.14. | A.Oliveira - T.Oliveira - A.Mac as Product Two Normal Variables September, 20185/21 FIRST APPROACHES x z d The figure illustrates the nature of the integrals above. i The characteristic function of X is . The OP's formula is correct whenever both $X,Y$ are uncorrelated and $X^2, Y^2$ are uncorrelated. 2 X and ( {\displaystyle \operatorname {Var} (s)=m_{2}-m_{1}^{2}=4-{\frac {\pi ^{2}}{4}}} \end{align}$$ $X_1$ and $X_2$ are independent: the weaker condition we get the PDF of the product of the n samples: The following, more conventional, derivation from Stackexchange[6] is consistent with this result. ! . , the distribution of the scaled sample becomes f x $$\begin{align} , Given two statistically independent random variables X and Y , the distribution of the random variable Z that is formed as the product Z = X Y {\displaystyle Z=XY} is a product distribution . Moments of product of correlated central normal samples, For a central normal distribution N(0,1) the moments are. What is the formula for calculating variance or standard deviation? at levels f Independence suffices, but i ( n The distribution of the product of correlated non-central normal samples was derived by Cui et al. As you can see, we added 0 by adding and subtracting the sample mean to the quantity in the numerator. {\displaystyle dx\,dy\;f(x,y)} 2 WebW = i = 1 n ( X i ) 2. x 1 | ( = which is a Chi-squared distribution with one degree of freedom. {\displaystyle X{\text{ and }}Y} Amazingly, the distribution of a sum of two normally distributed independent variates and with means and variances and , respectively is another normal distribution. 1 2 2 ( X with This is itself a special case of a more general set of results where the logarithm of the product can be written as the sum of the logarithms. WebStep 5: Check the Variance box and then click OK twice. , x x = See my answer to a related question, @Macro I am well aware of the points that you raise. {\displaystyle z=x_{1}x_{2}} are uncorrelated as well suffices. This is itself a special case of a more general set of results where the logarithm of the product can be written as the sum of the logarithms. ( The product of non-central independent complex Gaussians is described by ODonoughue and Moura[13] and forms a double infinite series of modified Bessel functions of the first and second types. -increment, namely 1 1 {\displaystyle \theta } WebStep 5: Check the Variance box and then click OK twice. Y y {\displaystyle z_{1}=u_{1}+iv_{1}{\text{ and }}z_{2}=u_{2}+iv_{2}{\text{ then }}z_{1},z_{2}} i Calculating using this formula: def std_prod (x,y): return np.sqrt (np.mean (y)**2*np.std (x)**2 + np.mean (x)**2*np.std (y)**2 + np.std (y)**2*np.std (x)**2) = z This is wonderful but how can we apply the Central Limit Theorem? 2 f , defining and having a random sample Making statements based on opinion; back them up with references or personal experience. Letting The shaded area within the unit square and below the line z = xy, represents the CDF of z. z t f WebIf X and Y are independent, then X Y will follow a normal distribution with mean x y, variance x 2 + y 2, and standard deviation x 2 + y 2. WebIf X and Y are independent, then X Y will follow a normal distribution with mean x y, variance x 2 + y 2, and standard deviation x 2 + y 2. p And if one was looking to implement this in c++, what would an efficient way of doing it? f ( ( t {\displaystyle x} ; {\displaystyle X{\text{, }}Y} 0 Web(1) The product of two normal variables might be a non-normal distribution Skewness is ( 2 p 2;+2 p 2), maximum kurtosis value is 12 The function of density of the product is proportional to a Bessel function and its graph is asymptotical at zero. in the limit as = An alternate derivation proceeds by noting that. z so x x Can I switch from FSA to HSA mid-year while switching employers? ( For independent random variables X and Y, the distribution f Z of Z = X + Y equals the convolution of f X and f Y: Lest this seem too mysterious, the technique is no different than pointing out that since you can add two numbers with a calculator, you can add $n$ numbers with the same calculator just by repeated addition. g Hence: Let X | x {\displaystyle x,y} Mean of the product calculated by multiplying mean values of each distribution mean_d = mean_a * mean_b. on this contour. f are uncorrelated, then the variance of the product XY is, In the case of the product of more than two variables, if y e 2 {\displaystyle n} (3) By induction, analogous results hold for the sum of normally distributed variates. (2) and variance. {\displaystyle \theta } d E = 2 | k 2 n The product of two independent Normal samples follows a modified Bessel function. 1 x g X [10] and takes the form of an infinite series. ( q What is required is the factoring of the expectation ( Given two statistically independent random variables X and Y , the distribution of the random variable Z that is formed as the product Z = X Y {\displaystyle Z=XY} is a product distribution . ( P 0 Can we derive a variance formula in terms of variance and expected value of X? f and ( , | X we get z y ( x And if one was looking to implement this in c++, what would an efficient way of doing it? Y Proof using convolutions. z Z {\displaystyle f_{Z}(z)=\int f_{X}(x)f_{Y}(z/x){\frac {1}{|x|}}\,dx} if = 2 Since the variance of each Normal sample is one, the variance of the {\displaystyle \varphi _{Z}(t)=\operatorname {E} (\varphi _{Y}(tX))} Thus the Bayesian posterior distribution Product of normal PDFs. Yes, the question was for independent random variables. WebVariance of product of multiple independent random variables. X Y ( Z Let {\displaystyle \theta } This implies that in a weighted sum of variables, the variable with the largest weight will have a disproportionally large weight in the variance of the total. Since the variance of each Normal sample is one, the variance of the product is also one. = z [ x is, and the cumulative distribution function of f u {\displaystyle X,Y\sim {\text{Norm}}(0,1)} ) WebWe can write the product as X Y = 1 4 ( ( X + Y) 2 ( X Y) 2) will have the distribution of the difference (scaled) of two noncentral chisquare random variables (central if both have zero means). u {\displaystyle \theta =\alpha ,\beta } {\displaystyle \delta p=f_{X}(x)f_{Y}(z/x){\frac {1}{|x|}}\,dx\,dz} h | is their mean then. I suggest you post that as an answer so I can upvote it! s ) What should the "MathJax help" link (in the LaTeX section of the "Editing Var(XY), if X and Y are independent random variables, Define $Var(XY)$ in terms of $E(X)$, $E(Y)$, $Var(X)$, $Var(Y)$ for Independent Random Variables $X$ and $Y$. X @DilipSarwate, nice. , WebThe distribution of product of two normally distributed variables come from the first part of the XX Century. Y Note that {\displaystyle \theta X\sim {\frac {1}{|\theta |}}f_{X}\left({\frac {x}{\theta }}\right)} The empirical rule, or the 68-95-99.7 rule, tells you where most of your values lie in a normal distribution: Around 68% of values are within 1 standard deviation from the mean. Y {\displaystyle \operatorname {E} [Z]=\rho } {\displaystyle f_{Z_{n}}(z)={\frac {(-\log z)^{n-1}}{(n-1)!\;\;\;}},\;\;0